Note sur l'illustration ci-dessus
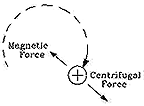
Beaucoup de livres donnent cet exemple mais disent que la corde est attirée vers le haut, alors que le pendule balance. C'est une situation plus complexe. En se balancant le pendule engendre une force centrifuge, et la traction sur la corde doit également surmonter la résistance de la force centrifuge, sans compter l'augmentation de l'énergie potentielle du fait d'amener le poids à une position moyenne plus élevée. Cela exige un apport supplémentaire d'énergie de la part de la force tirant la corde, et puisque l'énergie doit aller quelque part, l'oscillation du pendule est plus vigoureuse somewhere.
Cela ressemble un peu au cas de l'appui abaissé, mais le calcul donne un taux différent. Avec l'appui abaissé, un travail est également effectué -- mais se produit quand le poids atteint les extrémités de l'arc plus court qu'il parcourt, non au plus bas de l'oscillation.
Le processus décrit ici évoque les jeunes à la balançoire qui veulent aller le plus haut possible. L'enfant déplace ses bras, ses jambes et son corps pour lutter contre la force centrifuge, et l'énergie ainsi investie finit par produire un mouvement d'oscillation de plus en plus énergique.
(C'est une explication fortement simplifiée et suppose que du point de vue de l'oscillation de l'enfant, la nature se comporte exactement comme partout, et que seule la force centrifuge est en plus. La situation réelle peut être plus compliquée.)
En savoir plus Le musée de la science "Exploratorium" à San Francisco possède une petite balançoire (trop petite pour porter une personne) qui peut "être pompée" de l'extérieur. Le siège de la balançoire, au lieu de s'accrocher à deux cordes ou chaînes, est attaché à l'axe par deux tiges parallèles lisses.
Au-dessus du siège normal de la balançoire se trouve un deuxième siège, avec deux larges trous enfilés dans les deux tiges. Dans des circonstances normales, le deuxième siège repose sur l'autre. Cependant, une corde est reliée à sa partie médiane, passe au-dessus de la barre qui suspend la balançoire puis est dirigée vers le bas. Une personne se tenant à côté de la balançoire peut tirer cette corde ou la laisser descendre, réglant ainsi la position du siège le long des tiges.
A la main, vous avez poussé la balançoire dans un mouvement modéré. Maintenant, en tirant la corde ou en la laissant aller selon le rythme souhaitable vous pouvez facilement "accélérer" le mouvement. Il n'y a qu'à entraîner la balançoire quand elle passe la partie la plus inférieure de son mouvement, et la laissez s'abaisser aux extrémités de son déplacement, lorsque pendant un bref instant elle est immobile.
|
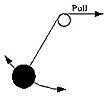 Dans la théorie des mouvements, c'est l'exemple d'un mouvement périodique dont la période diminue graduellement. Le mouvement périodique le plus connu est l'oscillation d'un pendule d'arrière en avant, par exemple un poids suspendu à une corde (dessin). Plus la corde est courte, plus la période de chaque oscillation ("période") est courte, proportionnellement à la racine carrée de la longueur. On peut remplacer le point d'attache par une de poulie, qui est graduellement abaissée et la corde se raccourcit (ignorez le mot "traction" pour des raisons expliquées ci-dessous). La course de l'oscillation reste la même, mais la période devient plus courte et plus courte.
Dans la théorie des mouvements, c'est l'exemple d'un mouvement périodique dont la période diminue graduellement. Le mouvement périodique le plus connu est l'oscillation d'un pendule d'arrière en avant, par exemple un poids suspendu à une corde (dessin). Plus la corde est courte, plus la période de chaque oscillation ("période") est courte, proportionnellement à la racine carrée de la longueur. On peut remplacer le point d'attache par une de poulie, qui est graduellement abaissée et la corde se raccourcit (ignorez le mot "traction" pour des raisons expliquées ci-dessous). La course de l'oscillation reste la même, mais la période devient plus courte et plus courte.