(E22) Electromagnetic Fields
The Electro-Motive Force
Oersted, Ampere and Faraday showed how an electric current could create a magnetic force. Joseph Henry, first secretary of the (then brand-new) Smithsonian Institution in Washington, DC, may have been the first to wrap a coil of insulated wire around an iron rod, connect the ends of the wire to a battery, and show that the rod became magnetized--an electromagnet, a useful device for electric doorbells and all sorts of applications. Seek an inverse process--wrap a coil of insulated wire around a bar magnet and check whether any current emerges from its ends--no, there isn't any.
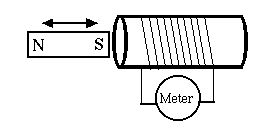
However, a magnet and an insulated coil could produce a brief burst of electric current in the brief instant when they were brought together. For instance, if the coil is wrapped around a cardboard tube, which is then quickly slipped over the bar magnet. The burst flowed in one direction when the tube was slipped on, and in the opposite direction when it was lifted off again. Current flows were reversed if connections to the coil were reversed, or when the poles of the magnet were exchanged before it was slipped on and off. It was a new way of generating an electric current. With a battery, a circuit started at one terminal of the battery and ended at the other, and the voltage clearly originated inside the battery by some chemical process. Here no specific location existed where the voltage originated, though in other ways it behaved like a battery's voltage, e.g. each part of the circuit satisfied Ohm's law. It was just that the voltage source was distributed around the circuit. Today we call such a distributed voltage an "electromotive force" or emf (ee-em-eff) for short, a term which actually goes back to Volta. It made no difference if the coil slid over the bar magnet or the bar was inserted into the coil. The process was named electro-magnetic induction and was discovered by Faraday in 1831. Faraday used a ring-shaped iron core, with two separate coils around it. When a current was driven through one coil (turning the core into an electromagnet), a "secondary current" briefly flowed through the second, and similarly if the current was turned off. Joseph Henry, secretary of the Smithsonian, may have observed induced currents at the same time, but did not follow it up. This was actually the first electric transformer, but transformers did not reach their practical and essential role until fifty years later, when alternating current was introduced. The idea of fieldsFaraday was more interested in the principle: what determined that spread-out voltage or "electro-motive force"? He found the answer, too--the variation with time of the "number of magnetic lines of force" threading the circuit, now commonly knows as "the magnetic flux." This somewhat novel terminology was associated with a changing view of electric and magnetic phenomena during Faraday's lifetime. Did such a thing exist as empty space? In early times, space which contained no material was deemed empty and devoid of properties. Today's definition is broader: properties are ascribed to space if something merely can be observed there: such space is called a field (or is said to contain a field). Space around the Sun is viewed as containing a gravitational field because, according to all that is know, if a grain of sand (say) were placed there, it would sense a gravitational pull and move accordingly. I do not know when scientists started using the term "field" to denote space modified by various causes. By the same argument, space modified by the presence of magnets or electric currents is a magnetic field, one modified by the presence of electric charges an "electric field," and when more complex interacting sources of electricity and magnetism are present, an "electro-magnetic field." The concept of fields helps balance inputs and outputs. The Sun and other stars emit energy (as light) at a tremendous rate. Where does that energy go? The small fraction which hits Earth provides life-maintaining heat and drives flows of air and water in the outer layers of Earth, but most of sunlight just keeps going into the darkness of space. By ascribing that energy to an electromagnetic field, energy is formally conserved. Mind you--this field is defined by forces which only may be sensed if some object is placed in their path. Is physics juggling the books on energy balance? Perhaps, but so far the idea of fields remains consistent. Does a tree falling in the forest make a sound if no one is listening? Does the answer make any difference? Field VectorsMagnetic "lines of force" (Faraday's term) or "field lines" (used nowadays) can describe a magnetic field, but mathematically they are hard to manage, Engineers and scientists working on electric and magnetic fields in "empty" 3-dimensional space prefer to use the electric field vector E and the magnetic field vector B. (When dealing with materials which modify electric and magnetic forces, these are replaced by D and H, but in our simplified coverage we assume no material involvement.) A vector, it its turn, is a quantity which has a direction in space as well as a magnitude--velocity is an example, also acceleration and force. Vectors may be viewed as 3-dimensional generalization of numbers--telling, for instance, not only how fast a bullet is fired, but also in what direction. They can be added and subtracted, as told in the section devoted to them (read it!), and also multiplied and generalized in several ways, mostly left undiscussed here. Vectors in equations are traditionally denoted by bold face letters, setting them apart from mere direction-les numbers ("scalars").
The electric field vector E is defined by the force F in Newtons on an electric charge of q coulombs. Yjat force is given by
and may be either in the direction of E if q is a positive charge, or in the opposite direction if q is negative.
Similarly, force on an isolated (north-seeking) magnetic pole of magnitude m in a magnetic field Bis
(We won't go now into definitions: m can be defined from the force of attraction or repulsion between two magnets, and the vector B is then defined by the above equation), A bar magnet always has two opposite poles (m) and (–m), so if B does not change significantly over the length of a compass needle (usual case) the magnetic forces on its poles are equal and opposite. Being equal, they do not try to move the entire needle bodily, but because they are applied to opposite ends, they will try to rotate it, until it points along the magnetic field line .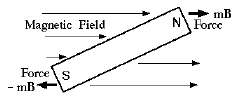 
Isolated magnetic poles have never been observed, but there also exists a magnetic force on the current I in a short electric conductor of length L (a vector!), equal to
where the multiplication mark (usually, within square brackets) denotes that this is a vector multiplication whose rules are
################################ Digression on Right and LeftOccasionally we need memorize which of two choices is the right one. If a current flows in a wire (plus to minus), do magnetic field lines produced by the current curl clockwise or counterclockwise? Faraday's rule of the right hand gives the answer: looking down on the thumb, counterclockwise.Actually, the answer depends on where one looks from: if you rotate your wrist and point the thumb down to the floor, the fingers point clockwise. If you have a clock with rotating hands and a transparent face, looking at it from the rear shows the hands rotating counterclockwise.
Mirror-writing is on a flat surface, Things are more complicated in 3 dimensions--just try wearing a right-hand glove on the left hand! Graphs on flat paper are usually drawn with the X-coordinate pointing right and the y-coordinate pointing ahead. But suppose we want to describe a figure in 3 dimensions, using a z-coordinate perpendicular to both axes. Which way should it point--up from the paper, or down into the paper?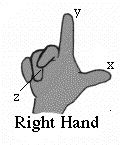 
Either choice is OK--but once made, we better stick to it. The common convention in mathematics is to work with right handed coordinates. Stretch the thumb, index and middle finger of the right hand until each is approximately perpendicular to the other two. Thumb, index, middle then give the axes of x, y and z. And that is also the order implied in vector multiplication, as given above: multiply thumb by index, the result is along the middle finger:
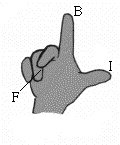If the current flows along the thumb and magnetic field lines point along the index, the magnetic force is along the middle finger.
There exist older rules for results like this--like Fleming's rule of the left hand--but maybe it's better to base it all on a mathematical convention everyone accepts nowadays. |