(8)   Electric Power     

Closed Circuits

    One big difference exists between our use of water and our use of electricity. Water indeed enters our homes along pipes, much the way electricity enters by wires. However, water is used in many different ways--cooking, washing, flushing waste, watering plants, adding humidity to the air. While the sewage pipes carry at least some of it out, the way it departs is not really a mirror image of the way it arrives.

    The way electricity leaves is essentially a mirror image of the way it arrives. True, in home wiring one side is "grounded" to the water lines and/or to metal stakes in the ground, but this is done for safety reasons, as discussed elsewhere. The wiring itself is symmetric: the "hot" wires that bring current into the house, covered in black or red insulation, are always matched by "return" wires that carry it back out, grounded and covered with white or green insulation. Electric charge enters and leaves at equal rates. As will be seen, it is pretty hard to store more than tiny amounts of electric charge.

    What the current does provide, between its coming and going, is energy .

   

Water flow can also, in principle, supply energy. Imagine electric power did not exist, and we needed something to drive machinery in the home--fans, tools, refrigerators, kitchen appliances and so forth. One way to get that energy would be to lead into the house a second system of water pipes, a closed system which is completely symmetric (drawing). Any water entering at high pressure P₁ leaves again at a lower pressure P₂, without leaving the system (compressed air could also serve). Connected to the pipes would be little water wheels, each with its on-off faucet, each with a shaft connected to part of the home's machinery, and the flow of water would turn the wheels. (Oscillating garden sprinklers actually do contain small waterwheels, to make them spray back and forth, and cover a rectangular area). Electricity, at least where it turns motors, acts very much like that.

    To remember:

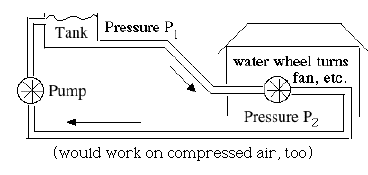
Watt's the Power?

    How much power W--that is, how much energy per second--is obtained from such a water wheel? We may guess it would be proportional to F, the amount of water flowing through it each second: double F and you double the power.

    We may also guess that it would be proportional to the pressure drop P = P₁ – P₂ which drives the wheel. Thus

with k some constant factor of proportionality, depending on the efficiency of the water wheel and also on the units in which F, P and W are measured. The efficiency may be ignored if W equals all the power produced, the useful power extracted from the wheel plus the power wasted by the friction of the machinery and the water, which turns into heat. (For more about "Pelton wheels" driven by water, see here.)

    For water wheels, the above formula is just a guess--W may be not be proportional to P but be derivable by some complicated expression involving P. The analogous formula for the power delivered by electric currents, however, holds exactly. If W equals all the power (see above) and common units are used, the factor k is not needed, and we get

    If I is measured in amperes and V in volts, then W is measured in watts (and now you also know the reason for using the letter W).

    How much is one watt? It is defined as 1 joule per second (see here for more about the joule: to lift a kilogram 10 centimeters takes about one joule). For comparison, 746 watt equal one horsepower (HP), and the output of the electric blower on your furnace blower is 1/4 or 1/3 HP. An athletic human can provide about 0.1 HP and a horse... actually, the steady output of the average horse is only about 0.7 HP. The unit was introduced by the Scottish inventor of the modern steam engine (in 1769), James Watt, who also introduced the concept of "power." Watt's early machines replaced horses which ran pumps for removing water from mines, and in measuring the output of a horse, Watt's man worked it extra hard.

    Sunlight falling perpendicularly on a square meter, neglecting loss to the atmosphere, carries about 1360 watts ("the solar constant"). Absorption and reflection may halve that amount, and the fact sunlight may arrive obliquely may halve it again, but still--there is a lot of energy in sunlight! Even with solar cells whose efficiency is only 10-15%, they are already the preferred source for some isolated users of electricity. The main problem is the high cost of solar cells, most commonly (though not exclusively) made of single crystals of silicon, carefully "grown" from a melt.

    The above formula holds for any energy output obtained from electricity. A 100-watt lightbulb, for instance, uses 100 watts of power to heat a thin filament, which then radiates some of it as visible light (and more of it as infra-red "heat rays"). If that bulb is plugged into a 110-volt house circuit (or more likely, alternating current (AC) with some average voltage of 110 volt), then the current I flowing through it satisfies