(E19) Electro-Magnetism

A more detailed story of early geomagnetism is collected in "The Great Magnet, the Earth"

Magnetic poles and electric charges at one time seemed rather similar: in each case, two kinds existed, opposites attracted and likes repelled. As Coulomb found around 1777, the forces between charges or poles always diminished with distance r like 1/r², which was also the way gravity decreased.

Yet there were differences. Magnetic poles always came in matched pairs, and steel needles could be magnetized by stroking them repeatedly in one direction by the pole of another magnet, or a natural "lodestone" magnet. Soft iron (like the kind used in paperclips and baling wire) also became magnetized when touched by a magnet, but this magnetization was temporary and ended when the magnet was removed.

The Earth itself was a giant magnet. This "geomagnetism" was a boon to sailors in mid-ocean, but magnetic north differed by a few degrees from astronomical north, and its direction slowly shifted over the decades. Edmond Halley--remembered for his comet--came up with an ingenious explanation of that slow variation: Earth consisted of layers, spheres within spheres, each magnetized differently and rotating slightly differently (it was more complicated than that).

Oersted

Then around 1800 Alessandro Volta invented the electric battery, and scientists in many countries began studying its electric currents. One was a Danish scholar, Hans Christian Oersted, professor of science in Copenhagen and personal friend of Hans Christian Anderson, spinner of folk tales--e.g. "the ugly duckling" and "the little mermaid".

One evening he invited a group of friends to his home, to show them some science demonstrations (more than one version of the story exists). With his "voltaic pile" he drove an electric current through a metal wire, showing that it heated up. On the same table, for another demonstration, he had a magnetic compass, and to his surprise he noted that every time the battery was connected, the magnetic needle rotated to a different position, returning to its north-south orientation when the current stopped. He did not point it out to his visitors, but after they left, he satisfied himself that the effect was real.

(A classroom demonstration using an opaque projector is described here.)

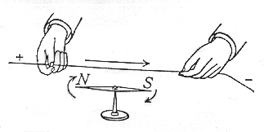What Oersted saw.

Yet he was unable to understand it. The needle was neither attracted to the wire nor repelled by it, but rotated, trying to point perpendicular to it. The rotation was in one direction with the needle above the wire, in the opposite direction below it, and reversing the battery connections also reversed the rotation. After experimenting for several months without reaching an explanation, he published a written report (in Latin!) in the science journals of his day, inviting other researches to confirm it and maybe puzzle it out.

The magnetic force could certainly be made stronger by winding the wire in a coil, which acted like a bar magnet. The magnetic effect was amplified even more if an iron rod was inserted in the coil (creating an "electromagnet") but even without any iron, the coil acted like a magnet, just not as strongly. Two coils lined up along the same axis attracted each other when the currents circulated in the same direction and repelled if the directions were reversed.

Oersted's Experiment.

Andre-Marie Ampére in France felt that if a current in a wire exerted a magnetic force on a compass needle, two such wires also should interact magnetically. In a series of ingenious experiments he showed that this interaction was simple and fundamental--parallel (straight) currents attract, anti-parallel currents repel. The force between two long straight parallel currents was inversely proportional to the distance between them and proportional to the intensity of the current flowing in each.

Only

not

₁

₂

₁

I₁ I₂ L₁ L₂/R²

(it gets further complicated if the currents flow in directions inclined to each other by some angle). To find then the force between wires of complicated shape that carry electrical currents, all these little bitty contributions to the force must be added up, which requires integral calculus. For two straight wires, the final result is as above--a force inversely proportional to 1/R, not to 1/R². This basic formula will be later revisited ]

Here is how this can lead to the notion of magnetic poles. Bend the wires into circles with constant separation (figure below):

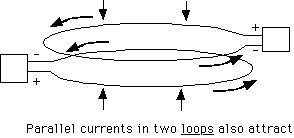Parallel currents in two loops also attract

--Two circular currents in the
same direction attract each other.

--Two circular currents in
opposite directions repel each other.

Replace each circle with a coil of 10, 100 or more turns, carrying the same current (figure below) and the attraction or repulsion increase by an equal factor. In fact, each coil acts very much like a magnet with magnetic poles at each end (an "electromagnet"). Ampere guessed that each atom of iron contained a circulating current, turning it into a small magnet, and that in an iron magnet all these atomic magnets were lined up in the same direction, allowing their magnetic forces to add up. (Nowadays one could claim that the electrons circling the nucleus carry such a current, but the actual situation is more complicated).

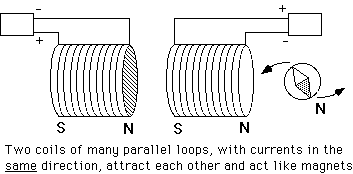
The magnetic property becomes even stronger if a core of iron is placed inside the coils, creating an "electromagnet"; that requires enlisting the help of iron, but is not essential.

(E20) Faraday and his "Lines of Force"

In our homes, cars, communications, computing and machinery, electric currents are are usually channeled by insulation wrapped around wires and boundaries.

On the other hand, mapping the structure of the Earth's magnetism across continents and oceans makes one think of effects spread out in space. Both channeled and unbounded phenomena exist and have their uses: information can be spread by both insulated telegraph wires and freely propagating radio waves. Two names stand out in the study of spread-out electric and magnetic phenomena in the 19th century: the Englishman Michael Faraday and the Scot James Clerk Maxwell--one an intuitive observer, the other a gifted mathematical scientist.

Michael Faraday was born in England I 1791, to a family of a blacksmith. His formal education stopped early, after which he was apprenticed to a bookbinder, giving cheap labor in return to learning a trade (Ben Franklin was similarly apprenticed to his brother, a printer). As books came to the shop to be rebound, Michael found opportunities to read them. Among them was a volume of the Encyclopaedia Britannica, summing up what was then known about electricity.

Anothe bright light of British science in the early 1800s was Humphry Davy, who "lived in the odium/of having discovered sodium." He did so by passing an electric current through molten table salt NaCl--salt dissolved in water would not do, because any sodium atoms separated break up water into hydrogen and oxygen, then recombine with the chlorine. He similarly separated potassium from its salt Kcl, also invented the extremely bright electric arc lamp, a safety lantern for coal miners and more.

Not long before that, the USA gained its independence from Britain, and one supporter of the crown ("tory") in that war was Benjamin Thompson of Rumford, near Boston. Thompson had to flee to England and later acquired the title "Count Rumford" in the service of a German prince. With some scientists, Rumford founded the "Royal Institution" in London for promoting science in Britain, and Davy gave there popular public lectures on the world of science. (The Royal Institution still exists, and includes now--among others--a museum devoted to Faraday).

Faraday managed to attend the lectures and kept detailed notes. When Davy fired an assistant for brawling, Faraday--now older--applied for the position, sending along his notebook as evidence of earnestness. He was hired, rose to become Davy's secretary and prime assistant, and in later years, his rival.

Magnetic Field Lines

Faraday's main asset was his clear intuition, which brought his lucid style in writing and lecturing. He also excelled in chemistry, kept detailed notebooks and was active in the Sandemanian church. To visualize magnetic forces, he imagined space around a magnet filled with a huge bundle of lines each of which, like a drawn arrow, had a definite direction, giving at any point the local direction of magnetic force. That is, the direction in which the north-seeking pole ("N pole") of a freely suspended compass needle would point, and in which a free-floating magnetic N-pole would be pushed by magnetic forces. He named them magnetic lines of force, though nowadays "magnetic field lines" is the usual term.

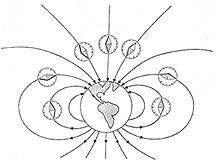
With the Earth's north-south magnetic force, these lines fan out from the vicinity of the south magnetic pole, arch above the (magnetic) equator and converge again in the region around the northern magnetic pole.

Lines of latitude and longitude on Earth are just a visualization--one can be drawn through any point on Earth. Were magnetic field lines like that too (but in three dimensions)? Faraday was not sure--a space filled with magnetic field lines did not seem to him empty any more.

This ambiguity still persists. Yes, they are just a visualization, pure mathematical abstractions. But they are also uniquely useful, in applications such as labeling the motion of electrons in space near a magnet. They seem to give only the direction of the magnetic force, not its strength--but their global configuration allows strength to be deduced, since they cluster more densely wherever the magnetic force is stronger. A related concept, "magnetic flux," is extremely useful in designing machinery. And yes, space around electric currents and charges, as we see it today, is not really empty but has specific properties (such as energy density). Today we call such modified space a "field"--a magnetic field, electric field or electromagnetic field. Many of these ideas started with Faraday's "lines of force," though (as discussed later) they were also foreshadowed by the study of fluids.

"Magnetic Rotations"

As Oersted demonstrated, an electric current in a wire also created magnetic forces, but in that case the field lines were closed loops around the current flow. Since compass needles tends to line up in the direction of the local field line, this explained why Oersted observed them trying to become oriented perpendicular to the wire. Field lines also trace the force on an isolated magnetic N-pole. Such isolated poles do not exist, but it is possible to observe forces on them if the corresponding S-pole is far enough to be hardly affected. In 1821, after Oersted had published his findings, Faraday (probably with Davy's advice) devised a clever experiment to do so.

In a goblet filled with mercury--a dense metal liquid at room temperature and conducting electricity--Faraday immersed a long iron bar magnet (iron floats in mercury). One end of the magnet (say, the S-pole end) was tied flexibly to a hook at the bottom, while the other floated up at an angle, poking out near the rim of the goblet. A vertical metal rod held by a stand poked into the middle of the goblet and connected to one side of a "voltaic pile" electric battery, while the other side was wired to the mercury at the edge of the goblet. When the circuit was closed, a current flowed through the rod, creating loops of field lines, and the floating N-pole end of the magnet circled around them.

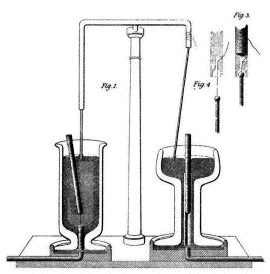
The S-pole in this case was tied down in one place, which served as pivot to the rotation. Reversing the battery connections reversed the rotation, as did exchanging the positions of the magnetic poles.

By Newton's 3rd law of mechanics, all forces act symmetrically: whenever the current exerts a force on a magnetic pole, the pole exerts an opposite and equal force on the current. This allowed Faraday to demonstrate the reverse process as well: the magnet was now vertically fixed along the axis of the goblet, while the rod conducting the current hung loosely from a supporting stand, at an angle, its tip floating near the edge of the goblet. This time, when the battery was connected, it was the rod that rotated around a cone. In a way, these were the first electric motors--though not very efficient ones, since the currents they required were rather large.

From experiments like this, Faraday devised his "right hand rule": stretch your right hand thumb and bend the other four fingers. If the thumb points in the direction of the current, the fingers curl the way field lines do around the wire.

(E21) Waves in Space

optional

Light

Allegedly it was Galileo who one night tried to measure the velocity of light, using two hooded lanterns and a helper. The helper with one lantern was posted at a far-away spot and was instructed to uncover his lantern the moment he saw light from Galileo's. When Galieo uncovered his lamp, the returning flash came almost instantaneously. He then told his helper to repeat the experiment at a much greater distance. The delay was just as short as before and Galileo concluded that is was mostly due to the reaction time of the helper, and that light spread very rapidly, maybe instantaneously.

The first actual estimate of the velocity of light in empty space was made in 1676 by Ole Roemer, a young Danish astronomer at the observatory of Paris, as a by-product of a method to determine longitude in mapping the Earth. It was a clever feat of deduction, but has already been described elsewhere in this collection, so the reader is encouraged to look up there

By the 1800s, a lot had been learned about light. Eyeglasses, telescopes and microscopes were in use--all based on the property that light slowed down in transparent materials. It was known to spread as a wave, propagating in empty space at about 300,000 km per second--a velocity nowadays denoted by the letter c--and slightly more slowly in air. A wave is a spreading disturbance associated with an oscillating phenomenon (mathematics has a more precise definition), giving it a wavelength λ (lambda, Greek lower case L), and a frequency ν = c / λ, the number of up/down oscillations per second when the wave passes any point in space (ν is nu, the Greek lower case N).

Sound is such a wave, an oscillation which can spread through air, water, walls and solids. Its wavelength can be inferred from the size of the instrument producing it, e.g. a plucked string--and the bigger the source, the longer the wavelength (centimeters to many meters) and deeper the sound (Big dog: woof, woof! Little dog: yip, yip!). Its velocity in air, demonstrated by the time lag between lightning and thunder, is about 330 meters per second.

Light also has its wavelength, but it is very small, as indicated by the sharpness of visible images. Only with very small objects, of size comparable to a wavelength, is the image fuzzed out. With half-closed eyes, in bright light, we see "floaters" in our eyeballs, specks of dust or short threads in the eyeball fluid, and these indeed are "fuzzed out" by wave effects, to tiny bright circles inside dark circles, or bright threads between dark parallel borders. The particles are actually too small for details to show up, all we see is the pattern of light waves they produce.

Microscopes and telescopes similarly have limited powers of magnification depending on wavelength, beyond which one only gets magnified blurs. Patterns of light that has passed a thin slit, the colors of patches of kerosene floating on water (whose thickness is comparable to the wavelength λ, dependent on color) or (these days) the colors reflected by the narrow grooves of a computer's compact memory disk--all these are related to the wave nature of light.

But what sort of wave? Sound does not spread in vacuum, but light does. Scientists in the 1800s therefore speculated that all space was filled with a "lumineferous (light carrying) aether" (will come back to that). A great achievement of 19th century was to show that light was linked to electricity--that it was an electromagnetic wave, part of a large family of such waves which grew with new discoveries to include infra red, ultra-violet, radio, microwaves, X-rays, gamma-rays and more.

Units of Electricity

The study of electricity in the 1800s uncovered an interesting relationship. The electrostatic law found by Coulomb, giving the force between electric charges q₁ and q₂ a distance r apart, was

F = k₁ q₁q₂/ r²

₁

Magnetic forces, on the other hand, allow one to define a unit of electric current i, by the force formula

F = k₂ i₁i₂ [ s₁s₂/ r² ]
giving the force between parallel wire elements of length s₁ and s₂ separated by a distance r. Ignore now the ratio in the square brackets--whatever units length is measured in, it remains the same (e.g. convert from inches to centimeters--any distance is multiplied by a factor 2.54, which then cancels out). If here F is again in Newtons and we choose k₂=1, this defines a natural unit of electric current i.

However, electric current and electric charge are related! A unit of electrical current should also correspond to a unit of electric charge moving at some velocity! Hidden somewhere in this haystack of units is a velocity which is a natural constant of nature.

It turns out to be the velocity of light c--possibly with factors like the ratio of the circumference of a circle to the diameter (π=3.141526...) which would actually be part of the formula. This may carry two kinds of message:

It turns out both hold true. Light is indeed an electromagnetic phenomenon, while c appears unexpectedly in formulas like Einstein's E = mc²

Note:

₁

₂

₀

"Ray Vibrations"

Sound in air is a pressure wave, advancing in the same direction as the force it produces. Light is altogether different, a "transverse wave" with effects in the directions perpendicular to its advancing front--like a sideways jiggling of a bowl of jelly pudding, or certain types of earthquake waves. Ordinary light vibrates in all directions, but certain crystals (known to Faraday) can separate vibrations into components polarized in two directions, perpendicular to the advance of light and to each other. The human eye can barely detect any difference, but Polaroid eyeglasses with crystals embedded in mutually perpendicular directions can separate two differently polarized images, and thus give us 3-D film images. Faraday also knew that light reflection from transparent surfaces (but not from ordinary mirrors with thin metal coating!) depended on the polarization of its components (in reference to the direction of the source), and that the blue color of the sky, from scattered sunlight, also had a preferred polarization, depending on the location of the Sun.

Polarized waves are somewhat like waves propagating on a long rope when one end is vigorously shaken. Shake the end up and down, and the waves are all in a vertical plane. Shake it sideways, and the waves are horizontal. And when the shaking is in random directions, so are the waves, though a vertical slit (like a polarizing crystal) will only allow vertical waves to pass, and a horizontal slit, only horizontal ones.

Faraday wondered if magnetic field lines filling space could oscillate like such ropes, and whether light, with its polarizations, consists of such oscillations. In April 1846 he gave an impromptu lecture Thoughts on Ray Vibrations on his speculations. In his report on the lecture, he wrote:

a kind of species of vibration in the lines of force

lateral

This beginning of the electromagnetic theory of light occurred in somewhat unusual circumstances. Faraday was schedule dto introduce a Friday lecture at the Royal Institution by Charles Wheatstone, remembered nowadays for his "Wheatstone bridge" for measuring electrical resistance (his talk however was on a timing device). Wheatstone came to the lecture hall, but developed an anxiety and left again before the talk began (allegedly, since the it has been customary at the Royal Institution to lock speakers in a room half an hour before the presentation).

With and audience but no speaker, Faraday gave the talk (he knew the subject), but with a lot of free time left at the end, added a talk about his own ideas. A hesitant speculation, not a polished talk, but that is what brand-new scientific ideas often look like. Once you know the answer, it may look deceptively simple and obvious; Faraday recaptures the uncertain mix of guess and hypothesis which precedes knowledge. He himself ended his report with these words:

I think it likely that I have made many mistakes in the preceeding pages, for even to myself, my ideas on this point appear only as the shadow of a speculation, or as one of those impressions on the mind which are allowable for a time as guides to thought and research. He who labours in experimental inquiries knows how numerous these are, and how often their apparent fitness and beauty vanish before the progress and development of real natural truth.

Today one might argue that Faraday was on the right path, but only at its beginning. It is true that oscillating magnetic field lines in a vacuum are just a mathematical abstraction. But the notion that they represent a possibility of magnetic force turned out to be the seed of the idea of fields in space.

But a key ingredient was still missing: because of magnetic induction, (discussed in what follows) there also existed an oscillating electric field--a possibility of sensing an electric force in the region where the wave is spreading.

The complete idea of an "electromagnetic wave" propagating in what is otherwise empty space was later correctly worked out by James Clerk Maxwell, and it fit all known properties of light; the velocity of propagation was a natural consequence of the two basic laws, cited above. And we no longer claim that the waves propagate in some "aether" filling space, because that would be a most unusual substance, one whose motion was unobservable. We just call the environment of propagation "space"--sometimes "space-time", or simply "the vacuum."

################################################

Thoughts on Ray Vibrations

Michael Faraday "Experimental Researches in Electricity", Vol III, M. Faraday, p447-452
also Philosophical Magazine, S.3, Vol XXVIII, N188, May 1846
Also on the web at http://www.padrak.com/ine/FARADAY1.html

To Richard Phillips, Esq.

Dear Sir,

At your request I will endeavor to convey to you a notion of that which I ventured to say at the close of the last Friday-evening Meeting, incidental to the account I gave of Wheatstone's electro-magnetic chronoscope; but from first to last understand that I merely threw out as matter for speculation, the vague impressions of my mind, for I gave nothing as the result of sufficient consideration, or as the settled conviction, or even probable conclusion at which I had arrived.

The point intended to be set forth for consideration of the hearers was, whether it was not possible that vibrations which in a certain theory are assumed to account for radiation and radiant phaenomena may not occur in the lines of force which connect particles, and consequently masses of matter together; a notion which as far as is admitted, will dispense with the aether, which in another view, is supposed to be the medium in which these vibrations take place.

You are aware of the speculation [M. Faraday, Phil Magazine, 1844, Vol XXIV, p136; or Exp.Res.II.284] which I some time since uttered respecting that view of the nature of matter which considers its ultimate atoms as centres of force, and not as so many little bodies surrounded by forces, the bodies being considered in the abstract as independent of the forces and capable of existing without them. In the latter view, these little particles have a definite form and a certain limited size; in the former view such is not the case, for that which represents size may be considered as extending to any distance to which the lines of force of the particle extend: the particle indeed is supposed to exist only by these forces, and where they are it is. The consideration of matter under this view gradually led me to look at the lines of force as being perhaps the seat of vibrations of radiant phenomena.

Another consideration bearing conjointly on the hypothetical view both of matter and radiation, arises from the comparison of the velocities with which the radiant action and certain powers of matter are transmitted. The velocity of light through space is about 190,000 miles in a second; the velocity of electricity is, by the experiments of Wheatstone, shown to be as great as this, if not greater: the light is supposed to be transmitted by vibrations through an aether which is, so to speak, destitute of gravitation, but infinite in elasticity; the electricity is transmitted through a small metallic wire, and is often viewed as transmitted by vibrations also. That the electric transference depends on the forces or powers of the matter of the wire can hardly be doubted, when we consider the different conductibility of the various metallic and other bodies; the means of affecting it by heat or cold; the way in which conducting bodies by combination enter into the constitution of non-conducting substances, and the contrary; and the actual existence of one elementary body, carbon, both in the conducting and non-conducting state. The power of electric conduction (being a transmission of force equal in velocity to that of light) appears to be tied up in and dependent upon the properties of the matter, and is, as it were, existent in them.

I suppose we may compare together the matter of the aether and ordinary matter (as, for instance, the copper of the wire through which the electricity is conducted), and consider them as alike in their essential constitution; i.e. either as both composed of little nuclei, considered in the abstract as matter, and of force or power associated with these nuclei, or else both consisting of mere centres of force, according to Boscovich's theory and the view put forth in my speculation; for there is no reason to assume that the nuclei are more requisite in the one case than in the other. It is true that the copper gravitates and the aether does not, and that therefore the copper is ponderable and the aether is not; but that cannot indicate the presence of nuclei in the copper more than in the aether, for of all the powers of matter gravitation is the one in which the force extends to the greatest possible distance from the supposed nucleus, being infinite in relation to the size of the latter, and reducing the nucleus to a mere centre of force. The smallest atom of matter on the earth acts directly on the smallest atom of matter in the sun, though they are 95,000,000 miles apart; further, atoms which, to our knowledge, are at least nineteen times that distance, and indeed in cometary masses, far more, are in a similar way tied together by the lines of force extending from and belonging to each. What is there in the condition of the particles of the supposed aether, if there be even only one such particle between us and the sun, that can in subtility and extent compare to this?

Let us not be confused by the ponderability and gravitation of heavy matter, as if they proved the presence of the abstract nuclei; these are due not to the nuclei, but to the force super-added to them, if the nuclei exist at all; and, if the aether particles be without this force, which according to the assumption is the case, then they are more material, in the abstract sense, than the matter of this our globe; for matter, according to the assumption, being made up of nuclei and force, the aether particles have in this respect proportionately more of the nucleus and less of the force.

On the other hand, the infinite elasticity assumed as belonging to the particles of the aether, is as striking and positive a force of it as gravity is of ponderable particles, and produces in its way effects as great; in witness whereof we have all the varieties of radiant agency as exhibited in luminous, caloric, and actinic phaenomena.

Perhaps I am in error in thinking the idea generally formed of the aether is that its nuclei are almost infinitely small, and that such force as it has, namely its elasticity, is almost infinitely intense. But if such be the received notion, what then is left in the aether but force or centres of force? As gravitation and solidity do not belong to it, perhaps many may admit this conclusion; but what are gravitation and solidity? certainly not the weight and contact of the abstract nuclei. The one is the consequence of an attractive force, which can act at distances as great as the mind of man can estimate or conceive; and the other is the consequence of a repulsive force, which forbids for ever the contact or touch of any two nuclei; so that these powers or properties should not in any degree lead those persons who conceive of the aether as a thing consisting of force only, to think any otherwise of ponderable matter, except that it has more and other forces associated with it than the aether has.

In experimental philosophy we can, by the phaenomena presented, recognize various kinds of lines of force; thus there are the lines of gravitating force, those of electro-static induction, those of magnetic action, and others partaking of a dynamic character might be perhaps included. The lines of electric and magnetic action are by many considered as exerted through space like the lines of gravitating force. For my own part, I incline to believe that when there are intervening particles of matter (being themselves only centres of force), they take part in carrying on the force through the line, but that when there are none, the line proceeds through space. Whatever the view adopted respecting them may be, we can, at all events, affect these lines of force in a manner which may be conceived as partaking of the nature of a shake or lateral vibration. For suppose two bodies, A B, distant from each other and under mutual action, and therefore connected by lines of force, and let us fix our attention upon one resultant of force, having an invariable direction as regards space; if one of the bodies move in the least degree right or left, or if its power be shifted for a moment within the mass (neither of these cases being difficult to realise if A and B be either electric or magnetic bodies), then an effect equivalent to a lateral disturbance will take place in the resultant upon which we are fixing our attention; for, either it will increase in force whilst the neighboring results are diminishing, or it will fall in force as they are increasing.

It may be asked, what lines of force are there in nature which are fitted to convey such an action and supply for the vibrating theory the place of the aether? I do not pretend to answer this question with any confidence; all I can say is, that I do not perceive in any part of space, whether (to use the common phrase) vacant or filled with matter, anything but forces and the lines in which they are exerted. The lines of weight or gravitating force are, certainly, extensive enough to answer in this respect any demand made upon them by radiant phaenomena; and so, probably, are the lines of magnetic force: and then who can forget that Mossotti has shown that gravitation, aggregation, electric force, and electro-chemical action may all have one common connection or origin; and so, in their actions at a distance, may have in common that infinite scope which some of these actions are known to possess?

The view which I am so bold to put forth considers, therefore, radiation as a kind of species of vibration in the lines of force which are known to connect particles and also masses of matter together. It endeavors to dismiss the aether, but not the vibration. The kind of vibration which, I believe, can alone account for the wonderful, varied, and beautiful phaenomena of polarization, is not the same as that which occurs on the surface of disturbed water, or the waves of sound in gases or liquids, for the vibrations in these cases are direct, or to and from the centre of action, whereas the former are lateral. It seems to me, that the resultant of two or more lines of force is in an apt condition for that action which may be considered as equivalent to a lateral vibration; whereas a uniform medium, like the aether, does not appear apt, or more apt than air or water.

The occurrence of a change at one end of a line of force easily suggests a consequent change at the other. The propagation of light, and therefore probably of all radiant action, occupies time; and, that a vibration of the line of force should account for the phaenomena of radiation, it is necessary that such vibration should occupy time also. I am not aware whether there are any data by which it has been, or could be ascertained whether such a power as gravitation acts without occupying time, or whether lines of force being already in existence, such a lateral disturbance at one end as I have suggested above, would require time, or must of necessity be felt instantly at the other end.

As to that condition of the lines of force which represents the assumed high elasticity of the aether, it cannot in this respect be deficient: the question here seems rather to be, whether the lines are sluggish enough in their action to render them equivalent to the aether in respect of the time known experimentally to be occupied in the transmission of radiant force.

The aether is assumed as pervading all bodies as well as space: in the view now set forth, it is the forces of the atomic centres which pervade (and make) all bodies, and also penetrate all space. As regards space, the difference is, that the aether presents successive parts of centres of action, and the present supposition only lines of action; as regards matter, the difference is, that the aether lies between the particles and so carries on the vibrations, whilst as respects the supposition, it is by the lines of force between the centres of the particles that the vibration is continued. As to the difference in intensity of action within matter under the two views, I suppose it will be very difficult to draw any conclusion, for when we take the simplest state of common matter and that which most nearly causes it to approximate to the condition of the aether, namely the state of the rare gas, how soon do we find in its elasticity and the mutual repulsion of its particles, a departure from the law, that the action is inversely as the square of the distance!

And now, my dear Phillips, I must conclude. I do not think I should have allowed these notions to have escaped from me, had I not been led unawares, and without previous consideration, by the circumstances of the evening on which I had to appear suddenly and occupy the place of another. Now that I have put them on paper, I feel that I ought to have kept them much longer for study, consideration, and, perhaps final rejection; and it is only because they are sure to go abroad in one way or another, in consequence of their utterance on that evening, that I give shape, if shape it may be called, in this reply to your inquiry. One thing is certain, that any hypothetical view of radiation which is likely to be received or retained as satisfactory, must not much longer comprehend alone certain phaenomena of light, but must include those of heat and of actinic influence also, and even the conjoined phaenomena of sensible heat and chemical power produced by them. In this respect, a view, which is in some degree founded upon the ordinary forces of matter, may perhaps find a little consideration amongst the other views that will probably arise.

M. Faraday,
April 15, 1846

Added note (DPS): Faraday was chairing a Friday lecture at the "Royal Institution," by Charles Wheatstone, on a device Wheatstone had invented for measuring very short time intervals (Wheatstone was also one of the originator of a British telegraph system). Half an hour before the talk the lecturer went home (for whatever reason), leaving Faraday with an assembled audience but no lecturer. [Since that time, allegedly, it has been a custom in the Royal Institution to lock speakers in an office half an hour before their talks]. Faraday knew enough about the subject to give a good account of Wheatstone's "chronoscope," leaving ample time to spare. To fill time, Faraday then added his own lecture, with the above title.

The text may be difficult, with ideas no longer held about the "aether" and the nature of atoms. Note however the indented paragraph, bringing out Faraday's main idea: magnetic field lines fill all space, and light propagating in space is a traveling wave, as if they were ropes shaken periodically at their ends. He felt such "transverse" waves, oscillating sideways like waves in molded gelatin ("jello"), explained the way light could be polarized.

The last paragraph is an example of Faraday's charming style.

################################################

(E22) Electromagnetic Fields

This section tries to introduce basic concepts without their mathematical details. Read carefully, but feel free to skip whatever seems dense (but not "remember the right hand").

The Electro-Motive Force

Oersted, Ampere and Faraday showed how an electric current could create a magnetic force. Joseph Henry, first secretary of the (then brand-new) Smithsonian Institution in Washington, DC, may have been the first to wrap a coil of insulated wire around an iron rod, connect the ends of the wire to a battery, and show that the rod became magnetized--an electromagnet, a useful device for electric doorbells and all sorts of applications. Seek an inverse process--wrap a coil of insulated wire around a bar magnet and check whether any current emerges from its ends--and no, there isn't any.

superconductors

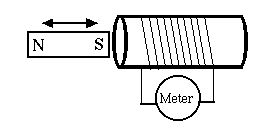
However, a magnet and an insulated coil could produce a brief burst of electric current in the brief instant when they were brought together. For instance, it the coil is wrapped around a cardboard tube, which was then quickly slipped over the bar magnet. The burst flowed in one direction when the tube was slipped on, and in the opposite direction when it was lifted off again. Current flows were reversed when connections to the coil were reversed, or when it was slipped on and off from the other end of the bar magnet.

It was a new way of generating an electric current. With a battery, a circuit started at one terminal of the battery and ended at the other, and the voltage clearly originated inside the battery by some chemical process. Here no specific location existed where the voltage originated, though in other ways it behaved like a battery's voltage, e.g. each part of the circuit satisfied Ohm's law. It was just that the voltage source was distributed around the circuit. Today we call such a distributed voltage an "electromotive force" or emf for short, a term which actually goes back to Volta.

It made no difference if the coil slid over the bar magnet or the bar was inserted into the coil. The process was named electro-magnetic induction and was discovered by Faraday in 1831. Faraday used a ring-shaped iron core, with two separate coils around it. When a current was driven through one coil (turning the core into an electromagnet), a "secondary current" briefly flowed through th second, and similarly if the current was turned off. Joseph Henry, secretary of the Smithsonian, may have observed induced currents at the same time, but did not follow it up. This was actually the first elctric transformer, but transformers did not reach their practical and essential role until fifty years later, when alternating current was introduced.

The idea of fields

Faraday was more interested in the principle: what determined that spread-out voltage or "electro-motive force"? He found the answer, too--the variation with time of the "number of magnetic lines of force" threading the circuit, now commonly knows as "the magnetic flux." This somewhat novel terminology was associated with a changing view of electric and magnetic phenomena during Faraday's lifetime.

Did such a thing exist as empty space? In early times, space which contained no material was deemed empty and devoid of properties. Today's definition is broader: properties are ascribed to space if something merely can be observed there: such space is called a field (or is said to contain a field). Space around the Sun can be deemed to contain a gravitational field because, according to all that is know, if a grain of sand (say) were placed there, it would sense a gravitational pull and move accordingly.

I do not know when scientists started using the term "field" to denote space modified by various causes. By the same argument, space modified by the presence of magnets or electric currents is a magnetic field, by the presence of electric charges an "electric field" and by more complex interacting sources of electricity and magnetism an "electro-magnetic field."

The concept of fields helps balance inputs an outputs. The Sun and other stars emit energy (as light) at a tremendous rate. Where does that energy go? The small fraction which hits Earth provides life-maintaining heat and drives flows of air and water in the outer layers of Earth, but the majority just keeps going into the darkness of space. By ascribing that energy to an electromagnetic field, energy is formally conserved. Mind you--this field is defined by forces which only may be sensed if some object is placed in their path. Is physics juggling the books on energy balance? Perhaps, but so far the idea of fields remains consistent. Does a tree falling in the forest make a sound if no one is listening? Does the answer make any difference?

Field Vectors

Magnetic "lines of force" (Faraday's term) or "field lines" (used nowadays) can describe a magnetic field, but mathematically they are hard to manage, Engineers and scientists working on electric and magnetic fields in "empty" 3-dimensional space prefer to use the electric field vector E and the magnetic field vector B. (When dealing with materials which modify electric and magnetic forces, these are replaced by D and H, but in our simplified coverage they will be avoided.)

A vector, it its turn, is a quantity which has a direction in space as well as magnitude--velocity for instance, or force. Vectors may be viewed as 3-dimensional generalization of numbers--telling, for instance, not only how fast a bullet is fired, but also in what direction. They can be added and subtracted, as told in the section devoted to them (read it!), and also multiplied and generalized in several ways, mostly left undiscussed here. Vectors in equations are traditionally denoted by bold face letters, setting them apart from mere direction-les numbers ("scalars").

The electric field vector E is defined by the force on an electric charge of q coulombs, which equals

F = qE
and may be either in the direction of E if q is a positive charge, or in the opposite direction if q is negative.

Similarly, the force on an isolated magnetic pole m (of the north-seeking kind) is

F = mB
A bar magnet always has two opposite poles (m) and (–m), so if B does not change significantly over the length of a compass needle (usual case) the magnetic forces on its poles are equal and opposite. Being equal, they do not try to move the entire needle bodily, but because they are applied to opposite ends, they will try to rotate it, until it points along the magnetic field line .

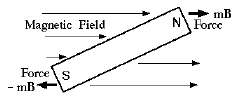
Isolated magnetic poles have never been observed, but there also exists a magnetic force on the current I in a short electric conductor of length L (a vector!), equal to

F = I [L × B]
where the multiplication mark (usually, within square brackets) denotes that this is a vector multiplication whose rules are

Multiply the magnitude of B by the component of L perpendicular to it (or else, the magnitude of L by the component of B perpendicular to it--the result is the same)
Multiply by the current intensity I
Assign to the result the direction perpendicular to both B and L, that is, perpendicular to the plane of these two vectors. Of the two opposite directions that qualify here, choose the one that satisfies Faraday's right hand rule.

If I is in amperes, L in meters and B in Teslas, then F is in Newtons.

Digression on Right and Left

Occasionally we need memorize which of two choices is the right one. If a current flows in a wire (plus to minus), do magnetic field lines produced by the current curl clockwise or counterclockwise? Faraday's rule of the right hand gives the answer: looking down on the thumb, counterclockwise.

Actually, the answer depends on where one looks from: if you rotate your wrist and point the thumb down to the floor, the fingers point clockwise. If you have a clock with rotating hands and a transparent face, looking at it from the rear shows the hands rotating counterclockwise.

does not

front

back

Mirror-writing is on a flat surface, Things are more complicated in 3 dimensions--just try wearing a right-hand glove on the left hand! Graphs on flat paper are usually drawn with the X-coordinate pointing right and the y-coordinate pointing ahead. But suppose we want to describe a figure in 3 dimensions, using a z-coordinate perpendicular to both axes. Which way should it point--up from the paper, or down into the paper?

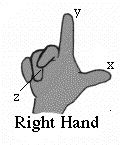
Either choice is OK--but once made, we better stick to it. The common convention in mathematics is to work with right handed coordinates. Stretch the thumb, index and middle finger of the right hand until each is approximately perpendicular to the other two. Thumb, index, middle then give the axes of x, y and z. And that is also the order implied in vector multiplication, as given above: multiply thumb by index, the result is along the middle finger:

I [L × B] = F

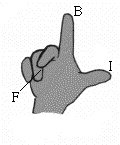If the current flows along the thumb and magnetic field lines point along the index, the magnetic force is along the middle finger.

There exist older rules for results like this--like Fleming's rule of the left hand--but maybe it's better to base it all on a mathematical convention everyone accepts nowadays.

(E23) Galvanometers

The Tangent Galvanometer

The simplest and earliest method of measuring electric current uses the tangent galvanometer. A flat coil of insulated wire is wound on a rigid frame, held by a stand in a vertical position. In the empty space in the middle of the coil a magnetic compass is mounted horizontally, and initially the coil is lined up so that is plane is vertical and in the north-south magnetic direction, the same as the magnetic needle.

Now insert the coil in the circuit being measured. The magnetic field of the current now tries to swing the needle 90 degrees, to point perpendicular to the coil. The position at which it settles will represent a balance between the north-south field of the Earth and the east-west force of the coil. That angle better be close to 45 degrees: If the effect of the coil overwhelms that of the Earth, accuracy is poor, though it can be improved by adding a known by-pass resistor so that (knowing also the resistance of the coil) only a known fraction of the current passes the coil. If the force of the coil is barely enough to move the needle off the north-south direction, the instrument is not sensitive enough.

This early instrument was not too practical, though students in labs may practice with it. It depends on the Earth's magnetism (whose accurate measurement was a separate task--first achieved by Gauss), which is variable and usually off-horizontal, its sensitivity depends on the coil and the current being measured still requires a calculation. Still, it provided an early application of Oersted's discovery.

Measuring the Magnetic Force

The force between two very short current segments dL₁ and dL₂ separated by a distance r decreases 1/r²

(the letter "d" in "dL" is calculus notation for "a very small part of L", and the directions of the vectors also count)

However, the force between fairly long parallel currents L₁ and L₂ (attraction when parallel, repulsion if opposed) only decreases like 1/r--one half at twice the distance, not one quarter-- the result of adding up an enormous number of small forces from each part of L₁ acting on each of an enormous number of parts of L₂.

Ampére actually measured the force between parallel currents, by comparing it against known weights in an ingenious "Ampére Balance". An instrument based on this force is the moving-coil galvanometer or D'Arsonval galvanometer, used to measure currents and voltages.

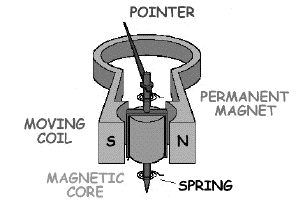
Its main components (be sure to identify the main ones before continuing!) are a strong permanent U-shaped magnet with concave pole pieced and a small rectangular pivoted coil ABCD, around which fine insulated wires are wound. The coil itself is shaped like a small flat box without top or bottom, and the pivot EE' crosses its middle, allowing it to rotate (to some extent) in the space between the pole pieces.

Other parts are insulated wires connected loosely to the coil (near the pivot, so as not to interfere with rotation, a pointer attached to the axle, with its tip in front of a dial indicating the current strength, a thin spiral spring defining the rest position of the pointer, and a small peg at the edge of the dial, stopping the pointer from moving too far--within (typically) 40-80 degrees of its rest position. The pole pieces end just short of the coil, and they channel the magnetic field lines to be perpendicular to the coil's positions. A cylinder of soft iron fills most of the space inside the coil and helps even out the magnetic field (and give more inertia to the coil).

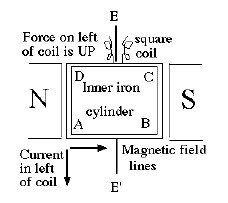
The operation is best understood if the rotating coil is viewed from above; let the current flow around the frame, in the direction (say) from A to B. With the magnet's polarity as drawn, by Faraday's rule of the right hand the magnetic force on the current will lift side AD and push down side BC. Since these are on opposite sides of the axis, the net effect would be to rotate the frame and its attached pointer, until the resistance of the spring stops it, at a position depending on the strength of the current. The forces on sides DC and AB do not contribute any rotation, they are parallel to the axle (plus, the currents are opposite so the forces cancel).

A sensitive galvanometer is useful for measuring either currents ("ammeter") or voltages ("voltmeter")--and the higher its sensitivity, the less it interferes with the circuit where measurement is made.

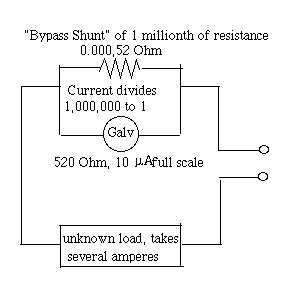
Suppose the full deflection corresponds to 10 microamperes (μA). Working as an ammeter, the galvanometer uses a choice of bypass resistors ("shunts") allows bigger currents to be measured. For instance, one having only a millionth of the resistance of the coil (or rather 1/999,999 of it--though lab instruments are not accurate enough for the difference to matter) multiplies the readings of the dial a million times--a deflection of a full dial now indicates 10 amperes. The instrument (including shunt) is inserted in series with the current being measured, and for very small currents, with no shunt, the resistance of the galvanometer must be taken into account.

On the other hand, suppose voltage between two points is measured. The instrument is connected "in parallel" between those points (drawing below) and includes a large resistor. The resistor greatly limits the current drawn from the main circuit, and thus minimizes the interference generated by the measurement.

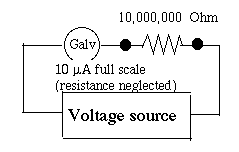
For instance, suppose our galvanometer with full deflection at 10 μA) has an added resistor of 10,000,000 Ω ahead of it. Now a voltage of 100 Volt will create a full-scale deflection, 20 volt a deflection of 1/5 of the dial, and so forth.

The above are the most traditional uses, and a laboratory "multimeter" will have a master switch to choose resistors in series or parallel, multiplying the dial's range by various powers of 10. It will also have a rectifier and filter for measuring AC, also internal batteries for measuring resistance, with appropriate settings of the master switch, and insulated cables for connecting it. This design, from the 19th century, is still widely used, although electronic multimeters are also being sold, based on solid-state devices and probably more rugged.

Afterthought: Electric Motors

Suppose we modify the instrument: omit the needle, the dial and its limiting peg, and attach the coil firmly to the axle. Would this create an electric motor?

No, not yet... but we are getting close! The wires leading to the coil should not get twisted, so they can't lead simply to the outside. Instead, cover a section of the axle with an insulating cylinder, and on it two metal rings, each divided in half by a small gap. The halves on one ring are connected to two ends of the coil in one order, on the other ring, in opposite order, and small leaf springs connect them to a battery.

Suppose the coil is connected so that the force rotates the axle clockwise. When the wires are pulled towards the poles of the magnet almost as far as they can go, the leaf springs encounter the gap and reverse the connection. Now the sections AD and BC are repelled by the pole closest to them, and attracted to the opposite one, and if a small flywheel keeps them spinning past the gap, the rotation will continue.

Some DC motors operate like this, but with greater efficiency. Why one square coil and not two perpendicular to each other for stronger force (The split ring will need more gaps), or even more? Why not fill the space inside the coils with iron, which concentrates the magnetic force? Why not replace the permanent magnet with an electromagnet, which can provide 4 regions of concentrated magnetic field lines, or more--to pull-repel the coil several times in the cycle? Why leaf springs and not carbon rods ("brushes") pushed by springs, for better and broader contacts?

Do all these and you will be well on the way to designing electric machinery. This section is not meant as an introduction to electric technology, so we stop here; but electric machinery has become a huge field, which keeps expanding. Electricity nowadays can drive cars, railroad engines, tanks and many other useful mechanisms, of all sizes.

Next Stop: Part 6

Home Page "All Things Electric and Magnetic"
"From Stargazers to Starships"
Timeline (from "Stargazers")
Master index file

Author and Curator: Dr. David P. Stern
Mail to Dr.Stern: stargaze("at" symbol)phy6.org .

Last updated: 8 July 2010