Le 3 leggi di Keplero sul moto planetario

    Quello che segue è il contenuto di una conferenza, tenuta il 23 marzo 2005, agli insegnanti di scienze di Anne Arundel County, Maryland. Viene presentata una panoramica delle tre leggi di Keplero con esempi, applicazioni, problemi e riferimenti storici. Si tratta di materiale utile per lezioni da svolgersi in classe.
    Sono riportati riferimenti e collegamenti alle relative sezioni del sito "Dagli astronomi alle astronavi". Agli insegnanti è stato anche distribuito il disco con tutto il materiale presente sul sito Web, così da poterlo utilizzare senza doversi collegare a Internet.

    Una guida rapida alle sezioni del sito "Dagli astronomi..." riguardanti le leggi di Keplero si può trovare nella sezione "Le leggi di Keplero". In quello che segue, le varie sezioni saranno talvolta indicate semplicemente con il loro numero. Si può comunque consultare la lista completa dei collegamenti, o facendo clic su "Mappa del sito" all'inizio di questa pagina, oppure su "Torna alla pagina iniziale", in fondo.

    Sul disco vi è molto più materiale di quanto possa essere mai trattato nelle vostre lezioni in classe. Ma voi siete insegnanti, e dovete avere una conoscenza più vasta, per poter selezionare il materiale adatto alle varie circostanze, e citare qualche piccola curiosità, senza discussioni dettagliate, ma soltanto per stimolare l'interesse degli studenti.

    E se siete molto fortunati, potreste talvolta trovare nella vostra classe uno o due alunni che veramente desiderano degli approfondimenti. In questi casi li potrete indirizzare qui, su questo sito Web, per una conoscenza più ampia.

    Fissiamo la nostra attenzione su tre argomenti:
---che cosa sono le leggi di Keplero, che cosa significano, e perché sono tanto importanti.

Le leggi sono state formulate tra il 1609 e il 16l9, e sono (come vengono in genere espresse):

1. I pianeti si muovono intorno al Sole lungo ellissi, di cui il Sole occupa uno dei fuochi.
2. La linea che va dal Sole al pianeta spazza aree uguali in tempi uguali.
3. Il quadrato del periodo orbitale di un pianeta è proporzionale al cubo (terza potenza) della sua distanza media dal Sole
       (o, in altre parole, del "semiasse maggiore" dell'ellisse, metà
       della somma della massima e della minima distanza dal Sole).

Il significato delle leggi di Keplero

    Le leggi di Keplero descrivono il moto dei pianeti attorno al Sole.
Ai tempi di Keplero erano noti 6 pianeti: Terra, Venere, Mercurio, Marte, Giove e Saturno.

L'orbita della Terra attorno al Sole. Questa vista è in prospettiva, la forma effettiva dell'orbita è molto prossima a una circonferenza.

    Tutti questi oggetti (compresa la Luna) si muovono quasi nello stesso piano (ved. sezione #2 del sito "Dagli astronomi..."). Il Sistema Solare è piatto come una frittella! Anche la Terra si trova sulla frittella, per cui noi vediamo l'intero sistema di profilo -- l'intera frittella occupa una linea (o quantomeno una sottile striscia) che taglia la volta celeste, e che è nota come l'eclittica. Tutti i pianeti, e anche il Sole e la Luna, si muovono lungo l'eclittica, o nelle sue vicinanze. Se vedete un gruppo di astri brillanti allineati lungo il cielo -- e nell'allineamento forse è compresa anche la Luna (la cui orbita è anch'essa prossima a quella "frittella"), o è posizionato vicino all'orizzonte dove il Sole è appena tramontato -- significa che probabilmente state vedendo dei pianeti.

    Gli antichi astronomi ritenevano che la Terra fosse al centro dell'universo, che le stelle fossero attaccate a una sfera che le ruotava attorno (noi oggi sappiamo che in realtà è la Terra che ruota) e che i pianeti si muovessero sulle loro "sfere cristalline" in modo strano. In genere i pianeti si muovevano nella stessa direzione, ma talvolta il loro moto si invertiva per un mese o due, e nessuno sapeva perché.

    Un ecclesiastico polacco, di nome Nicolò Copernico si rese conto nel 1543 che tutti quei movimenti acquistavano un senso se i pianeti si muovevano attorno al Sole, se la Terra era uno di essi, e se i più lontani si muovevano più lentamente, in modo che talvolta la Terra li sorpassava, per cui sembravano muoversi all'indietro per qualche tempo. Le orbite di Venere e di Mercurio si trovavano all'interno dell'orbita terrestre, per cui questi due pianeti non si muovevano mai lontano dal Sole. Questo è il motivo per cui non vedrete mai Venere a mezzanotte!

    Spero che descrivendo queste cose agli studenti -- la "frittella" dell'eclittica, il moto inverso ("retrogrado"), Venere sempre vicina al Sole -- riusciate a trasferire loro la sensazione visiva di questi pianeti nel cielo, che si muovono come astri luminosi sullo stesso percorso del Sole e della Luna. Le 12 costellazioni lungo quel percorso sono note come lo zodiaco, un nome che dovrebbe essere familiare a chi si interessa di astrologia. Venere, il più luminoso dei pianeti, oscilla avanti e indietro rispetto alla posizione del Sole, e così pure Mercurio, ma, poiché è molto più vicino al Sole, è possibile osservarlo soltanto quando si trova alla sua massima distanza dal Sole, e per appena qualche momento subito dopo il tramonto o prima dell'alba.

    Gli studenti avranno probabilmente sentito o letto che il Papa e la Chiesa hanno combattuto le idee di Copernico, poiché in uno dei Salmi (che in realtà sono delle preghiere in poesia) della Bibbia è scritto che Dio ha "fondato la terra sulle sue basi, e starà immota" (ediz. Paoline, 1961), (ma la più recente e più corretta traduzione della CEI riporta "mai potrà vacillare"). Galileo, uno studioso italiano, contemporaneo di Keplero, che sostenne le idee di Copernico, fu processato dalla Chiesa per disobbedienza e fu condannato agli arresti domiciliari per il resto della sua vita.

    Erano tempi in cui la gente spesso seguiva gli autori antichi (come il greco Aristotele) piuttosto che controllare con i propri occhi come funziona effettivamente la Natura. Quando si cominciò a verificare, osservare, sperimentare e calcolare, iniziò la rivoluzione scientifica. La nostra moderna tecnologia è l'ultimo risultato di questo processo, e le leggi di Keplero (insieme ai lavori di Galileo e a quelli sul magnetismo di William Gilbert) sono importanti, poiché da esse è iniziata quella rivoluzione.

Giovanni  Keplero

    Keplero lavorò con Tycho Brahe, un nobile danese che spinse l'astronomia pre-telescopica alla sua massima precisione, misurando la posizione dei pianeti quanto più accuratamente l'occhio umano potesse fare (Tycho morì nel 1602 a Praga, ora capitale della Repubblica Ceca; i telescopi iniziarono con Galileo attorno al 1609). Se volete approfondire l'argomento, vi raccomando il libro "Tycho e Keplero" di Kitty Ferguson, recensito sul sito http://www.phy6.org/outreach/books/Tycho.htm o quanto meno potreste leggere la recensione. Ne cito un brano:

    L'intolleranza religiosa era molto diffusa -- in effetti, gli eventi stavano andando verso la Guerra dei 30 anni (1618-1648), una delle più distruttive lotte religiose europee, rispecchiata nella guerra civile in Inghilterra. Keplero fu costretto ad abbandonare Graz, insieme a tutti gli altri impiegati dei collegi protestanti in città, dopo che l'arciduca al potere aveva decretato che essi dovevano lasciare la città prima di sera, quello stesso giorno. Era anche il periodo in cui la mamma di Keplero era stata arrestata per stregoneria, la maggior parte dei suoi numerosi figli erano morti in tenera età, e il matrimonio di Tycho era considerato come un'unione "slegfred" (concubinaggio) poiché la moglie scelta non era di stirpe nobile.

    Cercate anche di far capire agli studenti l'importanza di questi avvenimenti. L'anno 1620 era pure l'anno in cui i "Padri Pellegrini" sbarcarono a Plymouth Rock, cercando di sfuggire allo scoppio della guerra di religione che avrebbe, dopo breve tempo, devastato l'Europa. Molto probabilmente fu il ricordo di quelle guerre che portò gli Stati Uniti d'America, molti anni dopo, a decretare la separazione tra la Chiesa e lo Stato. Spiegate come lo sviluppo delle scienze e della società siano strettamente collegate.

La prima legge di Keplero

(1) I pianeti si muovono lungo ellissi, di cui il Sole occupa uno dei fuochi.

Occorre prima spiegare che cos'è un'ellisse: si tratta di una delle "sezioni coniche", quelle forme cioè ottenute tagliando un cono con una superficie piana. Una torcia elettrica genera un cono di luce: se la puntate contro una parete piana otterrete una sezione conica.

Colpite la parete perpendicolarmente. La parete taglierà il cono perpendicolarmente all'asse e si otterrà un cerchio di luce.

Inclinate il cono rispetto alla parete: si otterrà un'ellisse. Più inclinate la torcia e più lontano si richiuderà l'ellisse.

Le curve generate come  "sezioni coniche" quando  dei piani intersecano un cono.

Alla fine, quando un lato del cono è parallelo alla parete, la curva non si chiude più: avete ottenuto una parabola. Le leggi di Keplero (come le conosciamo ora) consentono tutte le sezioni coniche, e le parabole sono molto simili alle orbite delle comete non periodiche, che iniziano da molto, molto lontano.

(Inclinando ancora di più il fascio, otterrete un'iperbole -- non soltanto le traiettorie non si chiudono, ma le due direzioni di arrivo e di partenza divergono di un certo angolo).

    Vi sono ancora molte, molte altre cose... ma consideriamo ora soltanto due punti. Sono due punti adatti ad essere sviluppati in classe, poiché collegano il lavoro di Keplero attorno al 1610 con le ultime scoperte scientifiche del XXI secolo.
    Primo di tutti, osserviamo una famosissima ellisse mostrata nel disegno qui sotto. La storia è raccontata nella sezione #S7-a

    Probabilmente sapete tutti che il nostro Sole fa parte di un'immenso insieme di stelle a forma di disco --circa 100 miliardi di stelle, secondo le ultime stime-- chiamato galassia. E' un disco schiacciato, a forma di frittella, come il nostro Sistema Solare --e anche qui, noi vediamo questo disco di profilo, così che appare alla nostra vista come una sottile striscia. In questa striscia noi vediamo una fascia di deboli stelle che avvolgono tutta la volta celeste, la "Via Lattea".

    Che cos'è che tiene insieme la nostra galassia (e anche quelle molto più lontane)? Per molto tempo si è creduto che vi fosse un enorme buco nero al centro della galassia, ma che quel punto centrale fosse oscurato da nubi di polvere e che quindi non fosse facile da osservare. Recentemente, sono stati costruiti telescopi ad alta risoluzione, sensibili alla luce infrarossa, i quali riescono a vedere attravero la polvere, ed essi hanno mostrato una grande concentrazione di stelle in veloce movimento vicino al centro della galassia, in orbite che obbediscono alle leggi di Keplero. Il sito Web citato sopra mostra l'ellisse orbitale di una stella che orbita attorno al centro con un periodo di 15,2 anni, e con i calcoli si è ricavata una massa di circa 3,7 milioni di volte quella del nostro Sole, più o meno 1,5 milioni.

    [Riservato agli astronomi: la massa centrale aiuta a tenere insieme la galassia, ma vi sono tante altre masse coinvolte, per cui la rotazione delle parti più esterne della galassia non obbedisce alla terza legge di Keplero. Infatti le parti principali sembrano ruotare come se fossero dei dischi solidi, e questo è difficile da spiegare, a meno di supporre che la galassia contenga, oltre alle stelle visibili, anche una grande quantità di "materia oscura" che influenza la gravità ma non è visibile. Ved. la nota alla fine della sezione (20)].

    Secondo punto, abbiamo detto che la Terra orbita attorno al Sole (e, tra l'altro, la stessa legge vale anche per i satelliti artificiali in orbita attorno alla Terra). Ma immaginiamo ora di poter rendere gradualmente la Terra sempre più pesante e contemporaneamente rendere il Sole sempre più leggero. Che cosa succede? Quando il Sole e la Terra sono ugualmente pesanti, qual'è dei due corpi che orbita attorno all'altro?

    Circa 50 anni dopo Keplero, Isaac Newton diede una spiegazione delle leggi di Keplero (e così compì definitivamente la "rivoluzione scientifica", da quel momento in poi). Ecco che cosa fece:

---Primo, formulò le leggi fondamentali del moto, note da allora come le "3 leggi di Newton" (o "principi della dinamica"), e probabilmente è così che le insegnate ai vostri studenti.

---Secondo, ci diede la legge della gravitazione universale, mostrando che la stessa forza che fa cadere le mele e i sassi, è quella che mantiene la Luna nella sua orbita, e che ha prodotto tutti i moti orbitali del Sistema Solare.

    (Per saperne di più, anche a proposito della famosa mela, ved. la sezione #20).
http://www.phy6.org/stargaze/Igravity.htm )

--e Terzo, ha dimostrato che, in base ai due punti citati qui sopra, le leggi di Keplero possono essere ricavate matematicamente...

    ... ma con una piccola variante: i pianeti non orbitano attorno al Sole, ma attorno a un comune centro di gravità. Mentre la Terra compie un lungo percorso ogni anno, anche il Sole ne compie uno, molto più piccolo, attorno al centro di gravità Terra-Sole.

(in realtà, il Sole risente della presenza anche di Giove, Saturno, ecc... e la situazione risultante è piuttosto complicata).

    Perché tutto questo è importante? Perché ci aiuta a scoprire se altre stelle possiedono dei pianeti! Non possiamo vedere tali pianeti --troppo deboli-- ma se la stella ondeggia avanti e indietro in modo complicato, è perché c'è un pianeta che la fa muovere così.

    Ma il metodo funziona? Sì e no (ved. la fine della sezione #11a). Sono stati scoperti molti pianeti in questo modo, ma la maggior parte di essi sono troppo vicini alla stella (la durata delle oscillazioni è dell'ordine di settimane) e sono molto grandi. Scoprire pianeti di tipo terrestre è più difficile --l'ondeggiamento della stella sarebbe più piccolo e dovremmo fare osservazioni per molti anni per estrarre dai dati una periodicità dell'ordine di un anno. Ma abbiate pazienza, gli astronomi ci stanno lavorando.
------------------

La seconda legge di Keplero

(2) La linea che va dal Sole al pianeta spazza
        aree uguali in tempi uguali.

(Questa linea è chiamata talvolta il "raggio vettore").

Uno schema che illustra la seconda  legge di Keplero: i tratti di orbita AB  e CD sono percorsi in tempi uguali.

    Un'ellisse è un ovale allungato simmetrico, con due fuochi situati simmetricamente verso le estrtemità "più incurvate" -- in un fuoco c'è il Sole, l'altro è vuoto. (Provate a disegnare un'ellisse fatta così). Se avviciniamo sempre di più i due fuochi tra loro, l'ellisse tende a trasformarsi sempre di più in una circonferenza, e quando i due fuochi si sovrappongono, abbiamo esattamente una circonferenza.

    [L'orbita terrestre, come la maggior parte delle orbite planetarie, è molto prossima a una circonferenza. Se si guardasse l'orbita della Terra, senza il Sole nel fuoco, sarebbe molto difficile accorgersi che non è esattamente circolare. Con il Sole presente, tuttavia, ci si accorgerebbe che esso è un po' fuori centro.]

    L'aspetto importante della seconda legge di Keplero è che, nonostante l'orbita sia simmetrica, il moto non lo è. Un pianeta accelera quando si avvicina al Sole, raggiunge la massima velocità quando passa alla minima distanza, e poi rallenta di nuovo.

(La stella S2 raggiunge ben il 2% della velocità della luce quando si avvicina al buco nero al centro della nostra galassia).

    Si comprende meglio quanto accade in termini di energia. Quando il pianeta si allontana dal Sole (o un satellite dalla Terra), esso perde energia per vincere la forza di gravità, e quindi rallenta, come fa un sasso quando viene lanciato verso l'alto. E come il sasso, riguadagna la sua energia (completamente, non essendoci la resistenza dell'aria nello spazio) quando ritorna indietro.

    Vi è qui un utile esercizio, che è anche nella sezione #12A

    Supponiamo di avere un pianeta per il quale la minima e la massima distanza dal Sole siano r₁ e r₂ --esse corrispondono rispettivamente al perielio e all'afelio, se il centro del moto è il Sole, oppure al perigeo e all'apogeo, se il centro del moto è la Terra. (Le distanze sono sempre misurate dal centro dei corpi celesti, oppure dal centro di gravità).

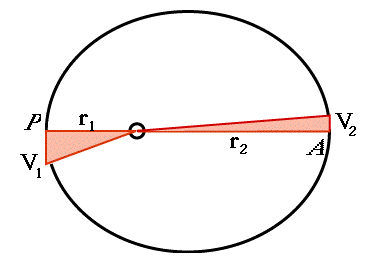
    Diciamo che si tratti di un pianeta in orbita attorno al Sole. Allora:
-- la velocità V₁ al perielio è la massima raggiunta nel suo moto orbitale. Corrisponde alla distanza percorsa in un secondo nei pressi del perielio.
-- la velocità V₂ all'afelio è la minima raggiunta, e corrisponde quindi alla distanza percorsa in un secondo nei pressi dell'afelio.

L'area spazzata dal "raggio vettore" r durante un secondo dopo il passaggio al perielio è quella di un triangolo rettangolo di base V₁, e che quindi è pari a 0,5 r₁ V₁.

L'area spazzata dal "raggio vettore" r durante un secondo dopo il passaggio all'afelio è quella di un triangolo rettangolo di base V₂, e che quindi è pari a 0,5 r₂ V₁.

Per la legge delle aree, le due aree sono uguali, per cui

    Se la distanza dell'afelio r₂ è 3 volte quella del perielio, la velocità V₂ all'afelio sarà 3 volte più lenta. (Nota: questa proporzionalità vale solo per questi due punti dell'orbita. Per gli altri punti la velocità e il raggio vettore non sono perpendicolari).
----------------

    Quando è che siamo più vicini al Sole? Attorno al 4 gennaio, di una quantità pari a circa l'1,5%, non abbastanza per notare una differenza nell'aspetto del Sole.
    C'è un metodo rapido per verificare questa asimmetria (benché potreste non avere tempo di trattarlo in classe). Disegnate un'ellisse con il suo asse maggiore e una linea perpendicolare ad esso passante per il Sole.
    Avviene (per puro caso) che gli equinozi di primavera e autunno, quando le durate del giorno e della notte sono uguali, in genere il 21 marzo e attorno al 22 o 23 settembre, cadano molto vicini a quella linea perpendicolare.

    Date un'occhiata allo schema dell'orbita terrestre nella sezione (3). L'asse maggiore (come definito precedentemente) è la linea che congiunge i punti contrassegnati con "Dicembre" e "Giugno" nel disegno, e la perpendicolare a quel segmento è la linea che congiunge "Marzo" con "Settembre".

    Se l'orbita fosse esattamente circolare (nel qual caso quello che chiamiamo "asse maggiore" sarebbe completamente arbitrario, in quanto tutti i diametri sono uguali), allora, per la seconda legge di Keplero, la Terra si muoverebbe a velocità costante e passerebbe lo stesso tempo nella metà estiva e nella metà invernale della sua orbita. In realtà, invece, la Terra sta due giorni in più nella metà invernale! (Prendete un calendario e contate i giorni che passano tra un equinozio e l'altro). Questo può significare che

   
• La metà invernale è più corta, oppure
• La Terra si muove più velocemente nella metà invernale

Effettivamente, sono vere tutte e due queste condizioni, se la Terra raggiunge la sua minima distanza dal Sole attorno al 4 gennaio. La "metà" dell'ellisse (determinata dalla linea perpendicolare definita qui sopra) che è più vicina al Sole è in realtà più piccola (lo si può verificare disegnando un'ellisse marcatamente ovalizzata), e, per la seconda legge di Keplero, la Terra si muove più rapidamente quando è più vicina al Sole.
-------------------------

    Il fatto che l'emisfero boreale è più vicino al Sole in pieno inverno ed è invece alla sua massima distanza dal Sole in estate, rende meno estreme le stagioni, facendole più miti.
    Nell'emisfero australe, le stagioni sarebbero più esasperate, ma la presenza dei vasti oceani attenua questo effetto.

    Però l'asse di rotazione della Terra si muove lungo un cono in circa 26000 anni. Fra 13000 anni saremo più vicini al Sole in piena estate, e il clima sarà più esasperato. Come è descritto nella sezione 7, questo effetto potrebbe essere collegato all'origine delle ere glaciali, ma non entreremo adesso in questi dettagli.

La terza legge di Keplero

(3) Il quadrato del periodo orbitale di un pianeta è
proporzionale al cubo della sua sistanza media dal Sole

(o, in altre parole, del "semiasse maggiore" dell'ellisse, la semisomma cioè della distanza massima e della distanza minima dal Sole)

    Questa è una legge matematica, e i vostri studenti avranno bisogno di una calcolatrice con le radici quadrate, le potenze frazionarie, come 3/2 e 2/3 (e magari anche le radici cubiche, o le potenze a 1/3)...

    Se due pianeti (o due satelliti della Terra, che è lo stessso) hanno periodi orbitali di T1 e T2 giorni, e distanze medie dal Sole (o semiassi maggiori) A1 e A2, allora la formula che esprime la terza legge è

    Gli studenti domanderanno subito: possiamo contare i giorni per sapere il periodo orbitale T (anche se può essere un po' malsicuro il conteggio, poiché dovremo sottrarre il contributo dovuto al moto della Terra attorno al Sole), ma come facciamo a conoscere la distanza A?

    In realtà, noi non la conosciamo, ma va notato che quello che occorre è solo il rapporto tra le distanze, e le unità di misura usate non influiscono su tale rapporto. Per esempio, supponiamo che il "Pianeta 2" sia la Terra, e che tutti i tempi siano misurati in anni. Allora T₂ =1 (anno) e possiamo anche misurare le distanze in Unità Astronomiche (UA), la distanza media Terra-Sole, per cui A₂ =1 (UA). La legge diventa allora, per ogni altro pianeta,