(35) Le astronavi

Collisioni elastiche

(Per semplificare il problema, assumiamo che la pallina da ping-pong sia "perfettamente elastica", e che quindi non perda energia quando rimbalza. Se esistesse una simile pallina e la facessimo cadere su un pavimento rigido, non solo rimbalzerebbe, ma risalirebbe esattamente alla stessa altezza dalla quale è stata lasciata cadere. Le reali palline da ping-pong non sono così perfette, ma un'astronave in una manovra di fionda planetaria, come nel caso che verrà discusso più avanti, lo è).

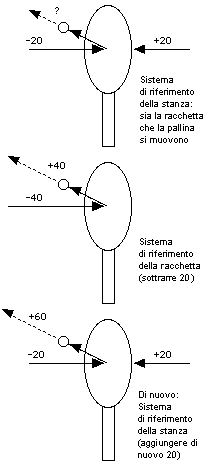
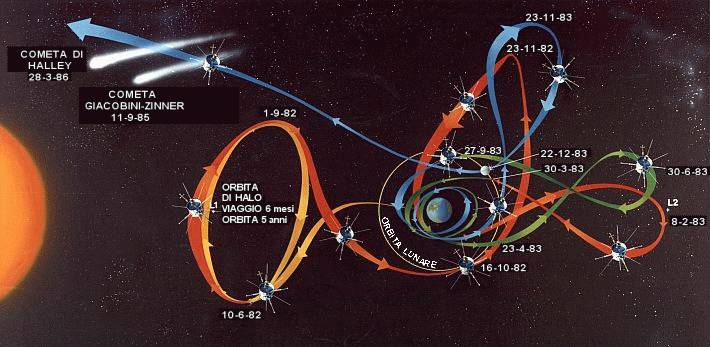
    In un problema di questo genere, con la pallina e la racchetta che si muovono entrambe con un certo angolo, occorre usare i vettori. Le collisioni frontali sono più semplici da trattare, poiché le velocità possono essere considerate positive in un verso e negative in quello opposto. Possiamo quindi immaginare in questo caso una pallina che viaggia a -20 mi/ora che urta contro una racchetta che si muove a +20 mi/ora (ved. la prima figura in alto; il rimbalzo è disegnato a un certo angolo, anche se in realtà avviene nella direzione opposta). Che cosa accade dopo?

    In ogni problema che coinvolga le forze, sommare la stessa velocità a tutti i moti non cambia la fisica del fenomeno. All'interno di un aereo di linea che viaggi a 1000 km/ora, un oggetto lasciato cadere, va giù dritto, come se si trovasse in una casa a terra. La ragione, naturalmente, è che aggiungendo una velocità di 1000 km/ora a tutti i moti, le accelerazioni (i cambiamenti di velocità) restano invariate, poiché, secondo le leggi di Newton, sono soltanto le accelerazioni che contano.

    Possiamo perciò sommare -20 mi/ora a tutte le velocità. La velocità della racchetta non è zero (e questo significa che anche noi ci muoviamo in modo solidale con essa, cioè che "siamo nello stesso suo sistema di riferimento"), mentre ora la pallina si muove a (-20) -20 = -40 mi/ora (ved. la figura al centro). Nella nuova situazione, una pallina che si muova a -40 mi/ora colpisce una superficie ferma; se la collisione è elastica (cioè non si perde energia), allora la pallina rimbalza con la stessa velocità ma in verso opposto, cioè con la velocità cambiata di segno. La velocità del rimbalzo è quindi +40 mi/ora.

    Infine ritorniamo al mondo reale, sommando +20 mi/ora a tutte le velocità. La racchetta ha ora di nuovo 0 + (20) = 20 mi/ora, la sua velocità originale, mentre la pallina ha una velocità di 40 +20 = 60 mi/ora. Urtando contro la racchetta in movimento, la pallina ha aumentato la sua velocità v del doppio della velocità della racchetta, e poiché l'energia cinetica è proporzionale a v², triplicando la sua velocità da 20 a 60 mi/ora, la pallina ha aumentato la sua energia di 9 volte! L'energia in più proviene dalla racchetta e dalla mano che la impugna.

   
Questo tipo di manovre viene spesso usato dalle sonde interplanetarie. Sono stati anche usati dei passaggi ravvicinati con la Luna, per inviare delle sonde verso i punti lagrangiani L1 e L2, per modificare delle missioni (come quella della "Geotail") e, il 22 dicembre 1983, per inviare dalla Terra la sonda ISEE-3 verso la cometa Giacobini-Zinner (la figura qui sopra descrive la sua orbita, che include vari incontri con la Luna, nelle date indicate). Sono stati anche usati per questo scopo degli incontri ravvicinati con la Terra stessa da parte della sonda spaziale Galileo, ora in orbita attorno a Giove: la sonda dapprima si è avvicinata a Venere, per poi tornare ad effettuare un passaggio radente vicino alla Terra. Tutto questo assomiglia a una sorta di biliardo cosmico, tranne che per il fatto che le "biglie", in questo caso le astronavi che effettuano gli incontri, sono dotate di piccoli motori a razzo, per correggere eventualmente la rotta e così rendere possibili dei percorsi molto complessi.

La prima sonda ad usare questo tipo di manovra è stata il Mariner 10, lanciato nel 1973 verso Venere, e che ha usato la forza di gravità del pianeta per estendere la sua orbita verso il pianeta Mercurio. La sonda Ulisse ha utilizzato un incontro con Giove per allontanare la sua orbita dal piano dell'eclittica e passare sopra entrambi i poli del Sole. Anche la "sonda solare," della NASA, che è prevista avvicinarsi entro 4 raggi solari al centro del Sole, userà una traiettoria a forma di "forcina per capelli" attorno a Giove.

  Un tenace sostenitore dell'uso delle manovre di "fionda planetaria" per viaggi economici tra la Terra e Marte è stato l'astronauta Buz Aldrin. Le sue idee sono descritte nell'articolo "A Bus Between the Planets" (Un autobus tra i pianeti) di James Oberg e Buzz Aldrin, p. 58-60, "Scientific American," Marzo 2000.

  Vi è un interessante parallelo tra le manovre di "fionda planetaria" e il funzionamento della turbina idraulica di Pelton. Dettagli in proposito si trovano nella sezione (35a), La fionda planetaria e la turbina di Pelton.

Verso le stelle

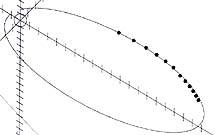
    Un incontro ravvicinato con un pianeta ha anche un'altra conseguenza: l'effetto della spinta dei razzi applicata nel momento del massimo avvicinamento al pianeta viene grandemente amplificato. Il progetto della missione "Profilo" verso la magnetosfera terrestre prevede una dozzina di piccoli satelliti posti inizialmente a bordo di "un'astronave madre" in una lunga orbita ellittica. Ad ogni passaggio ravvicinato ("perigeo") con la Terra, viene espulso un satellite, a una velocità non superiore a quella di un corridore a piedi. Tuttavia la spinta è sufficiente a farlo passare al perigeo, al prossimo passaggio ravvicinato, con un'ora di ritardo. Viene quindi espulso il prossimo satellite, e così via, uno per ogni passaggio. Alla fine tutti i satelliti saranno posizionati a un'ora di distanza l'uno dall'altro (ved. figura a destra) lungo una nuova orbita, che differirà leggermente dall'orbita dell'astronave madre. Questo è possibile con una semplice spintarella, ma che deve essere data nel punto giusto.

    Un giorno, in un remoto futuro, l'umanità probabilmente vorrà inviare delle sonde automatiche per esplorare le stelle lontane, con viaggi che potranno richiedere molte migliaia di anni. Molto tempo fa era stato suggerito che un buon metodo per raggiungere la velocità necessaria sarebbe stato quello di avvicinarsi dapprima al Sole, e poi nel punto di massimo avvicinamento accendere i razzi. Anche un modesto aumento di velocità vicino al Sole si sarebbe trasformato in un enorme aumento della velocità finale.

    Purtroppo questo metodo richiederebbe di arrivare piuttosto vicini al Sole, e la sonda spaziale probabilmente fonderebbe. Una partenza più ragionevole per una missione verso le stelle potrebbe essere da una cometa, poiché le traiettorie delle comete si estendono già ai confini del Sistema Solare, e il ghiaccio d'acqua presente nelle comete potrebbe fornire l'idrogeno e l'ossigeno come propellente per i motori dei razzi.

    In questo modo si potrebbero raggiungere le stelle più vicine alla Terra. Tuttavia, per arrivare alle regioni più lontane della galassia, potrebbero essere necessarie delle manovre di "fionda gravitazionale" come quelle proposte con il Sole. Esistono delle stelle nane che sono compatte come la Terra ma con una massa simile a quella del Sole, e forse se ne potrebbero localizzare alcune non più "accese", fredde e scure. In tal caso, una stella di questo tipo sarebbe un perfetto bersaglio per una manovra del genere. Al giorno d'oggi tutto questo è pura fantasia: ma l'umanità ha tempo, la sua avventura nello spazio è appena cominciata.

    Una nota recente: Secondo le ultime statistiche, le stelle nane di bassa luminosità sono sorprendentemente abbondanti nelle vicinanze del Sole, almeno il 60% del totale. Ved. la rivista Science, 11 Giugno 2004, pag. 1587.

Per saperne di più:

"The Starflight Handbook", Il manuale di astronautica, (dal sottotitolo: "A Pioneer's Guide to Interstellar Travel", Una guida per i pionieri dei viaggi interstellari), di Eugene F. Mallove e Gregory L. Matloff, John Wiley & Sons, 1989.

La sonda "Voyager 2" sta attualmente uscendo dal Sistema Solare. Nella remota possibilità che un giorno, in un lontano futuro, una civiltà aliena possa trovarlo, vi è stato posto un messaggio (ved. qui per maggiori dettagli).