#12e   Come si ricava l'Unità Astronomica

possono essere preparati in anticipo. Come è stato già mostrato, (R–r) = 15,25' (minuti d'arco), e per θ = 46,62° , si ha sin² θ/cosθ = 0,76124. Per le due stazioni di osservazione scelte in questo caso, con i tempi (ore:min:sec) espressi in Tempo Universale (ora di Greenwich), si ottiene dal sito

    Quando si tentò di usare per la prima volta il transito di Venere nel 1769, un inatteso fenomeno impedì di effettuare misure accurate di ΔT. Mentre il dischetto nero di Venere si avvicinava al bordo del disco solare, sembrò formarsi una specie di ponte scuro tra il dischetto nero e la zona scura al di là del disco solare, rendendo molto difficile stimare l'istante del secondo e del terzo contatto. La causa di questo "effetto della goccia nera" è ancora controversa, ma potrebbe essere connessa con la rapidissima diminuzione di luminosità del disco solare vicino al suo bordo. Questo "oscuramento del bordo" (che è anche evidente nell'immagine del Sole usata nella prima parte di questo calcolo) si verifica poiché la luce che ci arriva dal bordo visibile del Sole è necessariamente emessa sotto un angolo molto radente. Pertanto quella luce dovrà attraversare un grande spessore di strati solari più freddi (al di sopra della fotosfera, che è quella che emette la luce che vediamo, ma ancora al di sotto della cromosfera e della corona), ed è quindi in parte assorbita. Inserendo i precedenti valori nell'equazione (8) si ottiene (dove D è espresso in minuti d'arco):

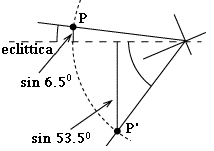
che è circa 1/3 della dimensione del dischetto di Venere davanti al Sole. Assumeremo che il percorso del transito sul disco solare sia parallelo all'eclittica, e quindi useremo soltanto la proiezione di PP' perpendicolare all'eclittica.

L'orbita terrestre

    Nel procedimento che verrà ora presentato, le distanze del Sistema Solare saranno espresse in unità astronomiche. La distanza media Terra-Sole è di 1 UA, ma varia leggermente a causa dell'eccentricità dell'orbita terrestre, e = 0,01673. (Questo valore può in linea di principio essere dedotto anche dalla differenza di durata delle stagioni, discussa nella sezione #12a a proposito della seconda legge di Keplero, ma non è un calcolo semplice). La distanza dal Sole di un pianeta che percorra un'orbita kepleriana, in coordinate polari (r, θ), è data da

(si noti che in questo caso il simbolo "r" è usato in modo diverso dal caso precedente). La (minima, massima) distanza si ha quando θ= (0°,180°) e cosθ = (1, –1). A causa dell'identità (1–e²) = (1–e)(1+e) tali distanze diventano r(1–e), r(1+e), o, se la distanza Terra-Sole è espressa in UA, semplicemente 1–e e 1+e.

    La Terra si trova alla sua minima distanza dal Sole (=al perielio) attorno al 4 gennaio, per cui si troverà alla sua massima distanza (all'afelio) all'inizio di luglio. Il transito di Venere dell'8 giugno 2004 era prossimo a questa seconda posizione, per cui possiamo supporre che la distanza Terra-Sole fosse di 1,015 UA (considerando che il valore all'afelio è di 1,01673 UA, dove raggiunge il massimo, e varia lentamente, fino ad arrivare a 1 UA all'equinozio di primavera, attorno al 21 marzo).

    Ma che cosa possiamo dire della distanza di Venere in UA? Qui ci viene in aiuto la terza legge di Keplero, secondo la quale il quadrato del periodo orbitale T è proporzionale al cubo della distanza media a (il semiasse maggiore). Il periodo di Venere è di 0,616 anni, da cui si ricava che la sua distanza media dal Sole è di 0,723 UA.

    Al momento del transito, Venere si trova tra noi e il Sole, e, se entrambe le orbite sono circolari, si deduce che la Terra si trova a 0,277 UA da Venere. In assenza di ulteriori informazioni, assumeremo che Venere abbia un'orbita circolare (in realtà è una buona approssimazione). Tuttavia, poiché la Terra è vicina all'afelio, con una distanza che abbiamo assunto pari a 1,015 UA, dobbiamo aggiungere altre 0,015 UA alla distanza Terra-Venere, ottenendo così 0,292 UA.

Lo spostamento della posizione apparente del Sole

Fig. 5   Il centro del Sole visto da P e da P'

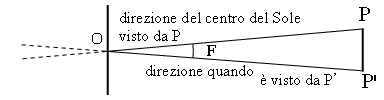
    Ora c'è un argomento un po' più delicato. Poiché P e P' si trovano a una certa distanza tra loro e il Sole non è a distanza infinita, la posizione di un punto sul Sole, rispetto alle stelle lontane (cioè misurata in coordinate sulla sfera celeste), è leggermente differente dalle due posizioni. Indichiamo con O il centro del Sole. Se il Sole fosse trasparente e potessimo vedervi le stelle attraverso, guardandolo da P e da P' si vedrebbe proiettato su uno sfondo leggermente diverso, e le due direzioni formerebbero un piccolo angolo F (ved. disegno). Le coordinate celesti di qualsiasi altro punto sul Sole (per esempio, una piccola macchia solare) mostrerebbero anch'esse questa differenza se l'osservazione fosse fatta da P o da P'.

    Indichiamo ora con x il numero di chilometri in una UA: è questo il numero che vogliamo ricavare! Il triangolo lungo e stretto PP'O può essere visto come una sottile sezione (come una fettina di torta) tagliata da un cerchio centrato nel punto O. L'intero circolo contiene 360×60 = 21600 minuti d'arco, e il rapporto tra F e quel numero è essenzialmente lo stesso del rapporto tra la distanza PP' (entro un piccolo errore dovuto al fatto che PP' è un segmento rettilineo) e l'intera lunghezza della circonferenza, che è 2πx, con 2π = 6,2832 con una precisione di 4 cifre decimali. Esprimendo tutto in cifre

    L'angolo F è molto piccolo, poiché il Sole è molto lontano. Tuttavia non può essere trascurato poiché anche l'angolo D con cui abbiamo a che fare è estremamente piccolo.

Fig. 6   Come va corretto l'angolo di vista per il Sole che si trova a distanza finita

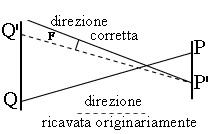
    Scegliamo ora un particolare istante, durante il transito, quando da P si vede Venere nel punto Q (sulla linea AB) e da P' si vede Venere nel punto Q' (sulla linea A'B'). Per questo calcolo, le posizioni nel cielo viste da P serviranno come nostro "sistema di riferimento", e le indicazioni "verso l'alto" e "verso il basso" si riferiranno alle direzioni nel disegno. Per ottenere le "direzioni standard nel cielo" per ogni punto del Sole visto da P' (incluso ogni punto di A'B', e in particolare Q') occorre "spostare verso l'alto" la sua posizione di un angolo F (ved. Figura 6).

L'angolo di parallasse corretto D'

Fig. 7   Schema della parallasse di Venere

    Per ottenere la "posizione nel cielo" di A'B' e di Q' nello stesso sistema di coordinate celesti usate per AB e Q, dobbiamo (come già notato prima) "sollevarla" di un angolo F verso il centro del Sole. Segue allora che l'angolo PVP' (o QVQ' che è lo stesso) non è D ma

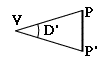
    Nella precedente sezione 12c, quando abbiamo discusso la Figura (1b), quell'angolo era indicato con "D", la qual cosa, come vediamo adesso, non è completamente corretta. Infatti l'angolo PVP' non era stato mai misurato, ma soltanto dedotto dalle posizioni osservate di Venere davanti al Sole. In realtà PVP' è uguale a D', non all'angolo D dedotto originariamente, poiché non soltanto Venere, ma anche il Sole, che si trova dietro, era stato osservato da due punti diversi.

    Ora in Figura 7 abbiamo un triangolo lungo e stretto, di cui un lato lungo è la distanza Terra-Venere, valutata a R_v = 0,292 UA. Poiché l'angolo D' è molto piccolo, PP' può essere approssimato a un piccolo arco di circonferenza, per cui

Possiamo applicare lo stesso ragionamento alla Figura 5, tranne che ora l'angolo è F e il lato lungo del triangolo è la distanza Terra-Sole, valutata a R_s = 1,015 AU.
Da cui (con ottima approssimazione)

Dal confronto delle due precedenti equazioni si ottiene

Dall'equazione (10)

Combinando le equazioni (11) e (12a),

Il valore di D era stato valutato pari a 0,310306 minuti d'arco. Dalla (12b) si ha

(Un ringraziamento al Prof. Udo Backhaus dell'Università di Essen per aver suggerito delle scorciatoie nei precedenti passaggi.)

Derivazione di PP'

    Durante il solstizio d'estate, attorno al 21 giugno, l'asse terrestre è inclinato verso il Sole, formando un angolo di 23,5 gradi con la retta perpendicolare all'eclittica. Con una approssimazione grossolana, possiamo assumere che era questa la situazione anche l'8 di giugno (ved. Figura 8a).

    Entrambe le località considerate si trovano a circa 30° ad est di Greenwich, per cui il loro tempo locale era avanti di due ore. Il transito quindi iniziava prima delle 8 di mattina e finiva verso l'una del pomeriggio. Al mezzogiorno locale di quel giorno, il raggio che va dal centro della Terra a P (Cairo) formava un angolo con l'eclittica (ved. disegno) di

e la distanza (perpendicolare) da P all'eclittica, in unità di raggi terrestri R_T, era

e la distanza (perpendicolare) di P' dall'eclittica era

Derivazione dell'UA

Fig. 8b   Proiezioni di P e P' perpendicolarmente all'eclittica

    La distanza tra i due punti, in direzione perpendicolare all'eclittica, che noi approssimiamo a PP' (trascurando lo spostamento dei punti nella direzione Terra-Sole, molto più piccolo della distanza di Venere e del Sole) era

    Alle 6 di mattina la linea PP' è orientata "di profilo" e il punto dell'equatore posto tra i due punti P e P' si trova anche sull'eclittica. Ripetendo i calcoli precedenti, si può dimostrare che gli spostamenti perpendicolari all'eclittica sono

La loro somma è

(si può ottenere lo stesso valore anche per via trigonometrica). Pertanto PP' è (per lo meno) quasi costante. Conocendo il raggio della Terra pari a 6371 km, otteniamo, con una accuratezza di 4 cifre decimali

Sostituendo nella (13),

Il valore riconosciuto attualmente è di circa 149,59 milioni di km (spesso arrotondato a 150 milioni), e pertanto il valore da noi ottenuto è giusto entro il 5%. (Non è il caso di cercare il motivo della discrepanza: un errore di 1 grado sul valore di θ porterebbe a un errore della stessa entità).

    Tra l'altro, gli astronomi spesso presentano questo dato in un modo equivalente, come la "parallasse solare". E' questo l'angolo F ottenuto nella Figura 5, se i due punti di osservazione sono separati da una distanza uguale a un raggio terrestre (1 R_T) e la distanza è di 1 UA. Il valore comunemente accettato per la parallasse solare è di 8,79" (secondi d'arco, 1/60 di minuto d'arco). Si può usare l'equazione (10) per ricavarla.