Mapa del sitio

(M-11)  Deducir el sen(α+β) y el cos(α+β)

Dadas las funciones (senα, cosα, senβ, cosβ), buscamos fórmulas que enuncien el sen(α+β) y el cos(α+β). La primera de esas fórmulas se usa para calcular los puntos lagrangianos L4 y L5, aquí.
 
 

¡Verifique, por favor, cada cálculo antes de proseguir!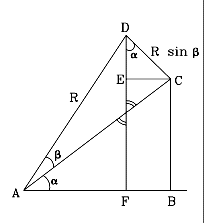

Como se muestra en el dibujo, para deducir la fórmula combinamos dos triángulos rectángulos
    ABC que tiene un ángulo α
    ACD  "      "      "     "    β
El lado mayor ("hipotenusa') de ACD es AD=R. Por consiguiente 
    DC = R sen β
    AC = R cos β
De modo semejante
     BC = AC sen α = R cos β sen α
    AB = AC cos α = R cos βcos α
El triángulo ADF es rectángulo y tiene el ángulo (α+β) . Por lo tanto
    R sen (α+β) = DF
    R cos (α+β) = AF

Comenzamos deduciendo el seno:

    R sen (α+β) = DF  =  EF + DE  =  BC + DE
  Observe en el dibujo los dos ángulos enfrentados señalados con líneas dobles: al igual que todos esos ángulos, deben ser iguales. Cada uno es uno de los ángulos agudos de su triángulo rectángulo. Como los ángulos agudos de ese triángulos suman 90 grados, los otros dos ángulos agudos deben ser iguales. Esto justifica el indicar el ángulo cerca de D como a, como se dibuja en la figura.

 En el triángulo rectángulo CED 

    DE = DC cos α = R sen β cos α
    EC = DC sen α = R sen β sen α
Anteriormente se presentó que
    BC = R cos β sen α
    AB = R cos β cos α
Por consiguiente

  R sen (α+β)  =  BC+DE  =  R cos β sen α + R sen β cos α

 Eliminando R y reacomodando α para que preceda β

    sen (α+β) = cos β sen α + sen β cos α

Del mismo modo, para el coseno

R cos (α+β) = AF = AB – FB = AB – EC =

        =  R cos β cos α – R sen β sen α

 Eliminando R y reacomodando

    cos (α+β) = cos β cos α – sen β sen α

 

Página principal en Español (índice)


Índice Matemático              Linea del Tiempo              Glosario .

Próxima Etapa:  #M-12   La Tangente

                          #M-11a    Ejercicios de Trigonometría

                           #34b  Los Puntos Lagrangianos L4 y L5

Author and Curator:   Dr. David P. Stern
     Messages to Dr.Stern:   stargaze("at" symbol)phy6.org   (English, please) .

Spanish translation by J. Méndez

Last updated 2 May 2005