|
Why triangles? Because they are the basic building blocks from which any shape (with straight boundaries) can be constructed. A square, pentagon or another polygon can be divided into triangles, say by straight lines radiating from one corner to all others.
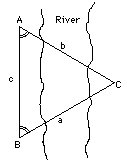
In mapping a country, surveyors divide it into triangles and mark each corner by a "benchmark", which nowadays is often a round brass plate set into the ground, with a dimple in its center, above which the surveyors place their rods and telescopes (George Washington did this sort of work as a teenager). After measuring a baseline--such as AB in the example of the river--the surveyor would measure (as described here) the angles it formed with lines to some point C, and use trigonometry to calculate the distances AC abd BC. These can serve as baselines for 2 more triangles, each of which provides baselines for two more... and so on, more and more triangles until the entire country is covered by a grid involving only known distances. Later a secondary grid may be added, subdividing the bigger triangles and marking its points with iron stakes, providing additional known distances on which any maps and plans can be based.
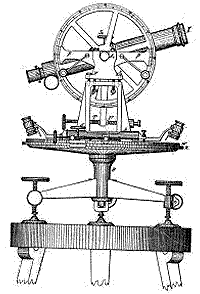
One large surveying project of the 1800s was the "Great Trigonometric Survey" of British India. The two largest-ever theodolites were built for the project, monsters with circular scales 36 inches wide, on which settings were read with exceptional accuracy by 5 microscopes. Each in its box weighed half a ton and needed 12 men for carrying it around. Using them, the project covered the country with multiple strings of triangles in the north-south and east-west directions (the areas between the strings were left for later) and it took decades to complete.
In 1843 Andrew Scott Waugh took charge of the project as Surveyor-General, and gave special attention to the Himalaya peaks north of India. Because of clouds and haze, those peaks are only rarely seen from the lowlands, and until 1847 few measured sightings were achieved. Even after they were made, the results had to be laboriously analyzed by "computers" in the survey's offices--not machines, but persons who performed the trigonometric calculations.
The story is told that in 1852 the chief computer, Radanath Sikhdar, came to the director of the survey and told him: "Sir, we have discovered the highest mountain in the world." From a distance of over 100 miles (160 km), the peak was observed from six different stations, and "on no occasion had the observer suspected that he was viewing through his telescope the highest point on Earth." Originally it was designated as "Peak XV" by the survey, but in 1856 Waugh named it after Sir George Everest, his predecessor in the office of chief surveyor. Everest was the one who commisioned and first used those giant theodolites; they are now on display in the Museum of the Survey of India in Dehra Dum.
Nowadays positions on Earth can be found pretty accurately using the global positioning system (GPS) of 24 satellites in precise orbits, constantly broadcasting their position. A small hand-held electronic instrument receives their signals and gives one's position within 10-20 meters (even more accurately for the military, the sponsor of the system). A great deal of trigonometry is involved, but it is all done for you by the computer inside your gadget, all you need do is push the proper buttons.
Now that you know a bit about the uses of trigonometry, you are welcome to advance to the actual nitty-gritty.
|