Site Map
Math Index
Glossary
Timeline
Questions & Answers
Lesson Plans
#M-10. Angles above 90°

(M-9) Deriving Sines and Cosines

Deriving the sine or cosine of an arbitrary angle takes a bit more math than is covered here. However, deriving them for a few special angles is relatively straightforward.

Complementary angles

    sNote first of all that a right-angled triangle contains two angles. Since all three angles (in any triangle) add up to 180°, the two sharp angles add up to 90°. It follows that if one of the angles is of A degrees, the other one (its "complementary angle") is (90°− A).

The sine and cosine were defined as the following ratios:

sin A = (side opposite to A)/(long side)
cos A = (side adjacent to A)/(long side)

Because the side opposite to A is the one adjacent to (90°– A), it follows that the sine of one angle is the cosine of the other, and vice versa:

sin A = a/c = cos (90° – A)
cos A = b/c = sin (90° – A)

This is a great help: deriving (for instance) the sine and cosine of 30°also gives us, as a bonus, the sine and cosine of 60°.

(1) A = 45°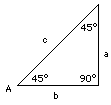

 If A = 45°, then also (90° – A) = 45°, and therefore
    sin 45° = cos 45°
Squaring
    sin2 45° = cos2 45°
However, it was found earlier that for any angle A
    sin2A + cos2A = 1
Therefore
    2 sin2 45° = 1

    sin2 45° = 1/2
and if √ means "square root of"
    sin 45° = √(1/2)
Pushing a button on your calculator gives
    sin 45° = 0.707107... = cos 45°
Another way, slightly more transparent, is to write
    sin2 45° = 1/2 = 2/4

    sin 45° = √2/√4 = √2/2
The square root of 2 is 1.4142135..., dividing it in two recovers 0.707107 as before.

(2) A = 30°, (90° – A) = 60°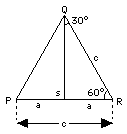

    Consider the triangle PQR (drawing) with all three angles equal to 60°. By symmetry, all three sides are equal too (a more rigorous proof exists, but we skip it). Drop a line QS perpendicular to PR: it divides the big angle into two right-angled triangles with sharp angles of (30°, 60°), which is the kind we are interested in. By symmetry, the triangles are of equal size and shape ("congruent") and therefore (skipping another proof)

    SR = (1/2) PR

In the notation of the drawing

    a = (1/2) c

    a/c = 1/2 = sin 30° = cos 60°
Continuing
    sin2 30° = 1/4
But
    sin2 30° + cos2 30° = 1
So
    1/ 4 + cos2 30° = 1

Subtract 1/4 from both sides

    cos2 30° = 3/4

    cos 30° = √3/ √4 = (√3)/2  =  1.7320508/2

    cos 30° = 0.8660254 = sin 60°

(3) A = 90° , (90° – A) = 0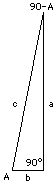

    It would be rather hard to draw a right-angled triangle with a second angle of 90° inside it, because the third angle then has to be 0°. But we can visualize this strange triangle as the limiting case of long skinny triangles with an angle A that is very steep and and its complement (90° – A) very small (drawing). In the limiting case

cos A = b/c = 0

and since

1 = sin2A + cos2A = sin2A + 0

it follows that

sin2A = 1     sin A = 1

Therefore

cos 90° = sin 0° = 0
sin 90° = cos 0° = 1

The full table then reads

A 0° 30° 45° 60° 90°
sin A 0 0.5 0.707107 0.866025 1
cos A 1 0.866025 0.707107 0.5 0

You should be able to draw a fairly good graph of sinA and cosA using the above points

(4) Postgraduate: A = 15°, (90° – A) = 75°

    The preceding derivations and table are standard fare in practically any course or text on trigonometry. You notice however the gaps between 0° and 30°, and between 60° and 90°. If we want the angle A to grow in equal steps of 15o, we still need the sine and cosine of 15° and 75°.

Are you interested? Here is how it can be done; hold on to your calculator!

    Draw a triangle ABC, with the angle A equal to 30° and the two bottom angles each equal to 75°. Then draw line BD perpendicular to AC (see drawing on the right). By symmetry, the sides AB and AC are of the same length; let that length be denoted by the letter a.

The triangle ABD has angles of 90, 60 and 30 degrees, and is therefore of the kind examined earlier. We get

BD = a sin 30° = 0.5 a
AD = a cos 30° = 0.866025 a

Then

DC = AC – AD = a – 0.866025 a = 0.133975 a

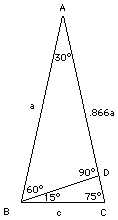
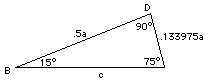Now look at the triangle BDC: its two larger angles equal 90° and 75°, forcing the remaining angle to be equal to 15°. Using the theorem of Pythagoras, if the long side is denoted c, we get

BD2 + CD2 = c2 = (0.5 a)2 + (0.133975 a)2
= 0.25 a2 + 0.0179493 a2 = 0.2679493 a2

Taking the square root

c = 0.517638 a

From that, to 5 decimals (and involving the complementary angle of 75° as well)

sin 15° = 0.133975/0.517638 = 0.25882 = cos 75°
cos 15° = 0.500000/0.517638 = 0.96593 = sin 75°

Now go and draw your graph!

Next Stop:   #M-10    Going Past 90 Degrees

Author and Curator:   Dr. David P. Stern
     Mail to Dr.Stern:   stargaze("at" symbol)phy6.org .

Updated 25 November 2001   Edited 28 October 2016