|
Given the functions (sinα, cosα, sinβ and cos β), we seek formulas that express sin(α+β) and cos(α+β). The first of these formulas is used in deriving the L4 and L5 Lagrangian points, here.
Please verify every calculation step before proceeding!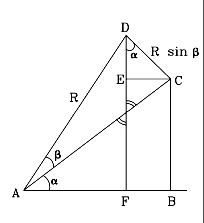 As shown in the drawing, to derive the formula we combine two right-angled triangles
As shown in the drawing, to derive the formula we combine two right-angled triangles
ACD which " " " β
AC = R cos β
AB = AC cos α = R cos β cos α
R cos (α+β) = AF Start by deriving the sine:
In the right-angled triangle CED
EC = DC sin α = R sin β sin α
AB = R cos β cos α R sin (α+β) = BC+DE = R cos β sin α + R sin β cos α Cancelling R and rearranging α to precede β sin (α+β) = cos β sin α + sin β cos α
Similarly, for the cosineR cos (α+β) = AF = AB –FB = AB –EC = = R cos β cos α – R sin β sin α Cancelling R and rearranging cos (α+β) = cos α cos β – sin α sin β
|