A site on the zodiac
On Polaris in the night sky: Finding the Pole Star
Next Stop: #2 The Path of the Sun, the Ecliptic
Two bright constellations occupy opposite sides of the pole star--the Big Dipper and
Cassiopeia. As the celestial sphere rotates (or appears to rotate), these constellations also march in circles around the pole . Depending on the hour of the night and the day of the year, one or the other may be low near the horizon where it is barely seen, or even hidden below the horizon. But when that happens the other constellation is sure to be high in the sky, where (weather permitting) it is easily seen.
The Big DipperThe Big Dipper consists of 7 bright stars, forming a dipper, a small pot with a long handle. In England it is often called "the plough" (spelled "plow" in the US), and fugitive slaves before the Civil War knew it as "the drinking gourd", a signpost in the sky pointing the way north to safety, to Canada where slavery was outlawed. Astronomers name it "Ursa Major," Latin for "the big bear," and some other languages also refer to it as the Big Bear.
The flag also shows how the north star can be found. Imagine a line connecting the two stars at the front of the "dipper", continue it on the side where the dipper is "open" to a distance 5 times that between the two stars (the flag shortens this a bit!), and you will arrive at (or very close to) the pole star. Because of their role in locating Polaris, these two stars are often called "the guides." And by the way--the last-but-one star in the handle of the "dipper", named Mizar by Arab astronomers, is a double star, whose components are readily separated by binoculars--or, some say, by very sharp eyes during good viewing conditions.
CassiopeiaCassiopeia was a queen in Greek mythology, and the constellation named for her is shaped like the letter W. Polaris is above the first "V" of this letter. If you draw a line dividing the angle of that "V" in half and continue along it, you will reach the vicinity of Polaris.The name of Cassiopeia's husband, King Cepheus, goes with a nearby constellation, above the other "V" (the brighter one), but Cepheus is nowhere as striking as Cassiopeia. Her daughter Andromeda has another constellation, framed by a big undistinguished rectangle of four stars. An unremarkable constellation to the eye--but it contains a large galaxy, our nearest neighbor in space (not counting two dwarf galaxies in the southern sky), one which seems to resemble ours in size and shape. Ursa Minor, the "Small Bear" or "Little Dipper" is a constellation somewhat resembling the Big Dipper, and Polaris is the last star in its tail. The "dipper" itself faces the tail of the Big Dipper, so that the two "tails" (or "handles") point in opposite directions. The two front stars of the "little dipper" (quite smaller and more square than the big one) are fairly bright, but other stars are rather dim and require good eyes and a dark sky.
|
 |
In summer, the Sun's path is longest, and so are the days. In winter, the Sun's path is shortest, and so are the days. |
Signs of the ZodiacEven though the planets move on the celestial sphere, they do not wander all over it but are confined to a narrow strip, dividing it in half. Stars along that strip are traditionally divided into the 12 constellations of the zodiac. The name, related to "zoo," comes because most of these constellations are named for animals--Leo the lion, Aries the ram, Scorpio the scorpion, Cancer the crab, Pisces the fish, Capricorn the goat and Taurus the bull. At any time, the Sun is also somewhere on the celestial sphere, and as the Earth turns, it rises and sets the same way as stars do. Like the planets, the Sun, too, moves around the zodiac, making one complete circuit each year. Every month it covers a different constellation of the zodiac, which is the real reason why those constellations are 12 in number. Of course, during that month, this particular constellation is not seen, because the sky near the Sun is too bright for its stars to be seen (except, very briefly, during a total eclipse of the Sun). One can however figure out where the sun is on the zodiac (as ancient astronomers have done) by noting which is the last constellation of the zodiac to rise ahead of the Sun, or the first to set after it. Obviously, the Sun is somewhere in between. In this manner each month-long period of the year was given its "sign of the zodiac." Astrologers, who believe that stars mysteriously direct our lives, claim it makes a great difference "under what sign" a person was born. Be aware, however, that the "sign" assigned to each month in horoscopes is not the constellation where the Sun is in that month, but where it would have been in ancient times. The difference is discussed in the section on the precession of the equinoxes The EclipticThe path of the Sun across the celestial sphere is very close to that of the planets and the moon. After clocks became available, it was a relatively straightforward job for astronomers to relate the path of the Sun in the daytime to the one of stars at night, and to draw it on their star charts. Because of its relation to eclipses, that path is known as the ecliptic.
The significance of the ecliptic is evident if we examine the Earth's orbit around the Sun. That orbit lies in a plane, flat like a tabletop, called the plane of the ecliptic (or sometimes just "the ecliptic"). In one year, as the Earth completes a full circuit around the Sun (drawing above), the Earth-Sun line and its continuation past Earth sweep the entire plane. The far end of that line then traces the ecliptic on the celestial sphere; if you have a star chart handy (it is often included in an atlas), you will find the ecliptic traced there, too. The Planets and the MoonPlanets seen in the sky are always near the ecliptic, which means that their orbits are never too far from the plane of the ecliptic. In other words, the solar system is rather flat, with all its major parts moving in nearly the same plane. What about the connection between "ecliptic" and eclipses? The moon's orbit cuts the ecliptic at a shallow angle, around 5 degrees, which means that on the celestial sphere the Moon, too, follows a path through the zodiac. Half the time the Moon is north of the ecliptic, half the time south of it. If the shadow of the moon hits the Earth, the Sun is eclipsed in the shadow area; if on the other hand the shadow of the Earth covers the moon, the moon goes dark and we have an eclipse of the moon. Either of these can only happen when the Sun, Earth and Moon are on the same straight line. Since the Sun and Earth are in the plane of the ecliptic, the line is automatically in that plane too; if the moon is also on the same line, it must be in the plane of the ecliptic as well. It takes close to a month for the Moon to go around the Earth ("month" comes from "Moon") and during that time its orbit crosses the ecliptic twice, as it goes from one side to the other. At the time of crossing, the Sun may be anywhere along the ecliptic; usually it is not on the Earth-Moon line, and therefore an eclipse usually does not take place. Occasionally, however, it is on that line or close to it. If it then happens to occupy exactly the same spot on the celestial sphere, we get an eclipse of the Sun, because the moon is then between us and the Sun. On the other hand, if it occupies the spot exactly opposite from that of the Moon, the Earth's shadow falls on the Moon and we have an eclipse of the Moon. Exploring FurtherA picture taken from the Moon showing three planets lined up along the ecliptic, as is the Sun.
|
Side trip: #2a Building a Sundial
Next Stop: #3 Seasons of the Year
########################
(Attributed to an essay by a student in elementary school.)
As the Sun rises, passes the highest point in its path (at noon and to the south, in the northern hemisphere) and sets, the shadow rotates around the stick in a clockwise direction, and its position can be used to mark time. Indeed, it has been claimed that the "clockwise" direction in which the hands on a clock rotate was chosen for this reason. A sundial with a vertical pointer ("gnomon") will indicate noon correctly when its shadow points north. However, the direction of the shadow at some other time of the day may depend on the season--its value in summer, when the Sun's path is high, may differ from what it is in winter, with Sun low above the horizon.
|
|
Such a sundial will however work equally well at all times if the pointer is slanted, to point towards the pole of the celestial sphere (click here for an explanation--but be warned, it is a bit complicated!). The angle between it and the base then equals the geographic latitude of the user.
A Paper SundialOrnamental sundials are often found in parks and gardens, with the pointer widened into a triangular fin, which must point northwards. A sundial of this type can be constructed from folded cardboard or stiff paper: click here to see the basic design, which can be printed and then photo-copied onto suitable sheets of stiff paper or cardboard [You may want to use the "option" menu to reduce size to 90% before printing--but make sure to return the setting to 100% afterwards!]. It is meant to be used at a latitude of 38 degrees and should work adequately in most of the continental US.
Note: In this printed version of many files together, the sundial plan must be on a page of its own, printed separately Instructions:
If you want to make a sundial of more durable materials, draw the pre-noon hour lines at the angles to the fin (given in degrees) given below. These lines are meant for a latitude of 38 degrees; if your latitude is markedly different, see note at the end.
|
| 6 -- 90° | 9 -- 31.6° |
| 7 -- 66.5° | 10 -- 19.6° |
| 8 -- 46.8° | 11 -- 9.4° |
AccuracyThe sundial will obviously be one hour off during daylight saving time in the summer, when clocks are reset.In addition, "clock time" (or "standard time") will differ from sundial time, because it is usually kept uniform across "time zones"; each time zone differs from its neighbors by one full hour (more in China and Alaska). In each such zone, sundial time matches clock time at only one geographical longitude: elsewhere a correction must be added, proportional to the difference in longitude from the locations where sundial time is exact.
Note on LatitudeThe angles listed above are intended for a latitude of 38 degrees. If your latitude is L, SQRT denotes "square root of" and K (=cotg2L) is
then the angle between the fin and the line corresponding to the hour N+6 (N going from 0 to 6) satisfies Here 15N (=15 times N) is an angle in degrees, ranging from 0 to 90, and of course, the afternoon angles are mirror reflections of the morning ones. If your calculator has a button (sin-1), if you enter (sin A) and press it, you will get the angle A. For an explanation of sines and cosines, look up the math refresher. And don't forget to adjust the angle of your fin to L, too!
|
The British Sundial Society also has its sundial page.
From the 1.1.2000 book catalog of Willman-Bell in Richmond, Virginia (www.willbell.com):
Next Stop: #3 Seasons of the Year
#######################
|
It is assumed here we are north of the equator, and the gnomon points to the north pole of the sky.
|
|
If the Earth's axis were perpendicular to the ecliptic, as in the drawings here, the Sun's position in the sky would be halfway between the celestial poles, and its daily path, seen from any point on Earth, would stay exactly the same, day after day.
Actually, the axis of rotation makes an angle of about 23. 5 degrees with the direction perpendicular to the ecliptic. That makes life a lot more interesting.
|
|
Twice a year, the angle is as big as it can get, at the summer and winter solstices, when it reaches 23.5 degrees. In the summer solstice (around June 21) the north pole is inclined towards the Sun, in the winter solstice (around December 21) it faces away from it. Let us look at the summer solstice first, with the Sun on the left.
|
Summer and WinterThe boundary AB between sunlight and shadow--between day and night--is always perpendicular to the Earth-Sun line, as it was in the example shown at the beginning.But because of the tilted axis, as each point on Earth is carried on its daily trip around the rotating Earth, the part of the trip spent in daylight (unshaded part of the drawing) and in the shadow (shaded) are usually not equal. North of the equator, day is longer than night, and when we get close enough to the north pole, there is no night at all. The Sun is then always above the horizon and it just makes a 360-degree circuit around it. That part of Earth enjoys summer. A mirror-image situation exists south of the equator. Nights are longer than days, and the further one gets from the equator, the larger is the imbalance--until one gets so close to the pole that the sun never rises. That is the famous arctic night, with 24 hours of darkness each day. In that half of the Earth, it is winter time. Half a year later, the Earth is on the other side of the Sun, that is, the Sun's position in the above drawing should be on the right, and the shaded part of the Earth should now be on the left (light and dark portions in the drawing switch places). The Earth's axis however has not moved, it is still pointed to the same patch of sky, near the star Polaris. Now the south pole is bathed in constant sunshine and the north one is dark. Summer and winter have switched hemispheres.
A big difference between summer and winter is thus the length of the days: note that on the equator that length does not change, and hence Spring, Summer, Fall, and Winter do not exist there (depending on weather patterns, however, there may exist a "wet season" and a "dry season"). In addition (as the drawing makes clear), the Sun's rays hit the summer hemisphere more vertically than the winter one. That, too, helps heat the ground, as explained further in section #4, "The Angle of the Sun's Rays." At equinox, the situation is as in the first drawing, and night and day are equal (that is where the word "equinox" comes from) Some interesting factsIf June 21 is the day when we receive the most sunshine, why is it regarded as the beginning of summer and not its peak? And similarly, why is December 21, the day of least sunshine, the beginning of winter and not mid-winter day? Blame the oceans, which heat up and cool down only slowly. By June 21 they are still cool from the winter time, and that delays the peak heat by about a month and a half. Similarly, in December the water still holds warmth from the summer, and the coldest days are still (on the average--not always! ) a month and a half ahead. And what about our distance from the Sun? It, too, varies, because the Earth's orbit around the Sun isn't an exact circle. We are closest to the Sun--would you believe it? --in the cold wintertime, around January 3-5. This may have an interesting implication for the origin of ice ages, as will be explained later. It also ties to an interesting story of the unusually bright Moon of December 22, 1999. |
Next Stop: #4 The angle of the Sun's Rays
#########################
 |
Note how much higher the Sun is in the sky in mid-summer! |
|
In the US and in other mid-latitude countries north of the equator (e.g those of Europe), the sun's daily trip (as it appears to us) is an arc across the southern sky. (Of course, it's really the Earth that does the moving.) The sun's greatest height above the horizon occurs at noon, and how high the sun then gets depends on the season of the year--it is highest in mid-summer, lowest in mid-winter. Boy scouts used to be taught (perhaps still are) that someone lost in the woods can often tell the north direction by checking on which side of tree-trunks moss grew best. Moss avoids direct sunlight, and with the sun's path curving across the southern sky, the north side of a tree-trunk is the one most shaded.
|
|
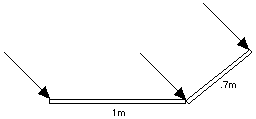
For a similar reason--but to collect sunlight rather than avoid it--solar collectors for heating water or generating electricity always face south. In addition, they are invariably tilted at an angle around 45°, to make sure that the arrival of the sun's rays is as close to perpendicular as possible. The collector is then exposed to the highest concentration of sunlight: as the drawing shows, if the sun is 45 degrees above the horizon, a collector 0.7 meters wide perpendicular to its rays intercepts as much sunlight as a 1-meter collector flat on the ground. It therefore heats its water faster and reaches a higher temperature. French wine producers, too, have for centuries preferred southward-facing hillsides, on which ripening grapes get the most sunlight.
|
|
The same also holds for the Earth. The rays of the summer sun, high in the sky, arrive at a steep angle and heat the land much more than those of the winter sun, which hit at a shallow angle. Although the length of the day is an important factor in explaining why summers are hot and winter cold, the angle of sunlight is probably more important. In the arctic summer, even though the sun shines 24 hours a day, it produces only moderate warmth, because it skims around the horizon and its light arrives at a low angle.
The apparent motion of the sun can be important in designing a building, in particular in the placing of windows, which trap the sun's heat. In a hot sunny climate such as that of Texas or Arizona, it is best to have the largest windows face north, avoiding the sun. The south-facing walls, on the other hand, should be well insultated and their windows should be small, allowing cross-ventilation when needed but not admitting much sunlight (wooden shutters on the outside of the windows also help). In Canada the opposite directions might be chosen, to trap as much heat as possible from the winter sun. Overhangs above south-facing windows also help. In summer, with the noontime Sun high in the sky, such an overhang casts a shadow on the window and keeps the house cool. In the winter, however, when the Sun stays close to the horizon, the overhang allows it to shine through the window and warm the rooms inside. |
Next Stop: #4a. The Moon: the Distant View
######################
|
The Moon's the North Wind's cookie He bites it, day by day Until there's but a rim of scraps That crumble all away. | The South Wind is the baker He kneads clouds in his den, And bakes a crisp new moon that ... greedy.... North.... Wind ....eats....again! |
| "What the Little Girl Said" Vachel (Nicholas) Lindsay, 1879-1931. |
The Month The monthly cycle of the moon (we won't capitalize the word here) must have mystified early humans--"waxing" from thin crescent ("new moon") to half-moon, then to a "gibbous" moon and a full one, and afterwards "waning" to a crescent again. That cycle, lasting about 29.5 days, gave us the word "month"--related to "moon," as is "Monday."
The monthly cycle of the moon (we won't capitalize the word here) must have mystified early humans--"waxing" from thin crescent ("new moon") to half-moon, then to a "gibbous" moon and a full one, and afterwards "waning" to a crescent again. That cycle, lasting about 29.5 days, gave us the word "month"--related to "moon," as is "Monday."The civil year, January to December, no longer ties its months to the moon, but some traditions still do and their terms for "month" reflect the connection--in Arabic, "shahr", in biblical Hebrew "yerach" and also "chodesh" from "new," since it was reckoned from one new moon to the next. Jericho (pronounced Yericho), one of the oldest cities on Earth, took its name from "yerach," and of course, legends tell of many moon-gods and goddesses, e.g. Artemis and Diana.
|
|
Early astronomers understood the different shapes of the moon, noting that each was linked to a certain relative position between moon and Sun: for instance, full moon always occured when moon and Sun were at opposite ends of the sky. All this suggested that the moon was a sphere, illuminated by the Sun. The moon's path across the sky was found to be close to the ecliptic, inclined to it by about 5 degrees. Eclipses of the Sun always occured when moon and Sun were due to occupy the same spot in the sky, suggesting that the moon was nearer to us and obscured the Sun. Eclipses of the moon, similarly, always occured at full moon, with the two on opposite sides of the Earth, and could be explained by the shadow of the Earth falling on the moon. Lunar eclipses allowed the Greek astronomer Aristarchus, around 220 BC, to estimate the distance to the moon (see section #8c). If the moon and the Sun followed exactly the same path across the sky, eclipses of both kinds would happen each month. Actually they are relatively rare, because the 5-degree angle between the paths only allows eclipses when Sun and moon are near one of the points where the paths intersect. . The cycle from each new moon to next one takes 29.5 days, but the actual orbital period of the moon is only 27.3217 days. That is the time it takes the moon to return to (approximately) the same position among the stars.
|
 Why the difference? Suppose we start counting from the moment when the moon in its motion across the sky is just overtaking the Sun; we will call this the "new moon," even though the thin crescent of the moon will only be visible some time later, and only shortly after sunset. Wait 27.3217 days: the moon has returned to approximately the same place in the sky, but the Sun has meanwhile moved away, on its annual journey around the heavens. It takes the moon about 2 more days to catch up with the Sun, to the position of the next "new moon," which is why times of the new moon are separated by 29.5 days.
Why the difference? Suppose we start counting from the moment when the moon in its motion across the sky is just overtaking the Sun; we will call this the "new moon," even though the thin crescent of the moon will only be visible some time later, and only shortly after sunset. Wait 27.3217 days: the moon has returned to approximately the same place in the sky, but the Sun has meanwhile moved away, on its annual journey around the heavens. It takes the moon about 2 more days to catch up with the Sun, to the position of the next "new moon," which is why times of the new moon are separated by 29.5 days.
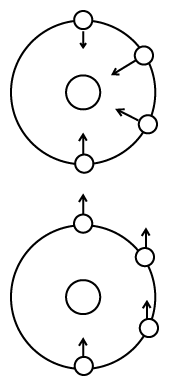
The Face of the MoonThe visible face of the moon has light and dark patches, which people interpreted in different ways, depending on their culture. Europeans see a face and talk of "the man in the moon" while children in China and Thailand recognize "the rabbit in the moon." All agree, however, that the moon does not change, that it always presents the same face to Earth.Does that mean the moon doesn't rotate? No, it does rotate--one rotation for each revolution around Earth! The drawings on the left, covering half an orbit, should make this clear. In them we look at the moon's orbit from high above the north pole, and imagine a clock dial around the moon, and a feature on it, marked by an arrow, which initially (bottom position in each drawing) points at 12 oclock. |
|
In the top drawing the marked feature continues to point at Earth, and as the moon goes around the Earth, it points to the hours 10, 8 and 6 on the clock dial. As the moon goes through half a revolution, it also undergoes half a rotation
If the moon did not rotate, the situation would be as in the bottom drawing. The arrow would continue to point in the 12-oclock direction, and after half an orbit, people on Earth would be able to see the other side of the moon. This does not happen. We need to go aboard a spaceship and fly halfway around the Moon before we get a view of its other side--as did the Apollo astronauts who took the picture below.
The Gravity GradientThis strange rotation of the moon is maintained because the moon is slightly elongated along the axis which points towards earth. To understand the effect we look at the motion of a body with a much more pronounced elongation--an artificial satellite with the shape of a symmetric dumbbell (drawing).It can be shown that if the forces on the dumbbell (or indeed on a satellite of any shape) are unbalanced, it rotates around its center of gravity. That point will be defined later, but in a symmetric dumbbell with two equal masses marked A and B, the center of gravity is right in the middle between them. |

Of course, if it started from an off-equilibrium position, it can overshoot the mark and then swing back and forth around equilibrium, like a pendulum. The elongated moon acts like a dumbbell too, and does in fact swing a little from side to side, like a pendulum of like balanced scales; this has allowed astronomers even before the space age to see a little more than half the moon. Such motion is known as "libration," from " libra", balance-beam scales--also the name of a constellation of the zodiac and of an ancient unit of weight, from which our abbreviation lb is derived. The rotating force which lines up the moon or an orbiting dumbbell therefore depends not on how strongly gravity pulls it, but on how rapidly the pull of gravity changes with distance--on the "gravity gradient." Near Earth that is a gentle force, though it is strong enough to line up elongated satellites. Among those was Triad, shaped like a long dumbbell with an additional payload in the middle, the first satellite to map the electrical currents associated with the polar aurora. It did swing back and forth with a 6-minute period, complicating the analysis of its data. Near a black hole or pulsar, on the other hand, the gravity-gradient force is fierce enough to rip a spacecraft apart.
|
Next Stop: #4b The Moon: A Closer Look
###########################

(4b) The Moon: A Closer LookThe View Through the Telescope
Giovanni Riccioli in 1651 named the more prominent features after famous astronomers, while the large dark and smooth areas he called "seas" or "maria" (singular "mare," mah-reh). Some of the names he used for the Moon's crater are of persons discussed in "Stargazers"--Tycho (distinguished by bright streaks that radiate from it), Ptolemy ("Ptolemaeus"), Copernicus, Kepler, Aristarchus, Hipparchus, Erathosthenes; Meton and Pythagoras are on the edge, near the northern pole. Late-comers who lived after the 17th century had to make do with left-overs: the craters Newton and Cavendish are at the southern edge of the visible disk, Goddard and Lagrange too are near the edge. Also, "Galilaei" is a small undistinguished crater (because of Galileo's banishment?). However, since the Russians were the first to observe the rear side of the Moon, a prominent crater there bears the name of Tsiolkovsky, who at the end of the 19th century promoted the idea of spaceflight.
The Craters
|

We now know that the impact explanation was right. The craters are round because at the enormous velocities with which meteorites arrive, the impact resembles a local explosion, and the signature of the impact is determined by the energy released rather than by the momentum transmitted.
Part of the evidence has come from the nicely rounded impact remnants found on Earth, e.g. Meteor Crater (Canyon Diablo) in Arizona and Manicougan lake in Canada, in northern Quebec (picture on left), which is about 100 km (60 miles) wide and 214 million years old. Note that rather than having a pit in its center, the Manicougan lake has a round island. After the impact, the land rose again to the level of its surroundings, pushed by fluid pressure of the material below it, which acts like a viscous fluid and tries to establish equilibrium between the different loads which it supports. (For another picture of Lake Manicougan, and more about it, click here.) Other solid bodies of the solar system also diplay round craters. On the large ice-covered moons of Jupiter, the return to equilibrium is much more pronounced, because ice sags and flows much more readily than rock. Those moons display "palimpsest" craters which are merely surface markings, because as time passed, the walls which originally existed sagged back onto the flat surface.
|
The Airless MoonIn the centuries after Galileo's discoveries, the Moon was extensively studied by astronomers using telescopes. One thing soon became clear: it had no atmosphere. When a star was eclipsed by the Moon, it vanished suddenly and its light showed no refraction or absorption by an atmosphere.Why? By the laws of motion, the Moon orbits not the center of the Earth, but the center of gravity of the Earth and Moon (this will be discussed in section #11a, and the center of gravity is defined in section #25). The location of that point allows astronomers to deduce the mass of the Moon, and from that, the pull of the Moon's gravity. At the surface of the Moon, it turned out, gravity is only 1/6 as strong as at the surface of the Earth. Gravity is important for the retention of an atmosphere. It holds an atmosphere down, while heat is what can make it escape. Heat is atomic or molecular motion. In a hot solid or liquid, it can be viewed as a shaking motion of atoms or molecules around their average position, like the rustling of leaves in a wind. The higher the temperature, the more vigorous the motion, until the material boils or evaporates, at which point its particles shake loose altogether. In a gas atoms and molecules fly around randomly, colliding constantly (if the gas is as dense as it is in the atmosphere), and their collisions lead to a very good explanation ("the kinetic theory of gases") of the observed properties of a gas. The average velocity of a gas molecule depends on the temperature of the gas, and at room temperature it is comparable to that of the speeding bullet, quite below the "escape velocity" needed for escaping Earth's gravity. However, that is just an average: actual velocities are expected to be distributed around that average, following the "Maxwellian distribution" first derived by James Clerk Maxwell, whom we meet again in the discovery of the three color theory of light (section #S-4) and the prediction of electromagnetic waves (section #S-5). According to that distribution, a few molecules always move fast enough to escape, and if they happen to be near the top of the atmosphere, moving upwards and and avoiding any further collisions, such molecules would be lost. For Earth, their number is too small to matter, but with the Moon, having only 1/6 of the surface gravity, it can be shown that any atmosphere would be lost within geological time. The planet Mercury, only slightly larger, also lacks any atmosphere, while Mars, with 1/3 the Earth's surface gravity, only retains a very thin atmosphere. Water evaporates easily and once in gas form, is quickly lost by the same process. That suggested the "maria" could not possibly be oceans, though their name remained. They actually turned out to be basaltic flows, hardened lava which long ago flowed out of fissures on the Moon; no present-day volcanism on the Moon has been reliably identified. The vast majority of craters probably date back to the early days of the solar system, because the lava of the maria has very few craters on it, suggesting it flooded and obliterated older ones. The picture of a dry Moon was reinforced by Moon rocks brought back by US astronauts. Earth rocks may contain water bound chemically ("water of hydration"), but not these. Water, of course, would be essential to any human outpost on the Moon. Yet small amounts of water may still exist, brought by comets which occasionally hit the Moon. All this water is sure to evaporate in the heat of the collision, but some of it may re-condense in deep craters near the Moon's pole, which are permanently in the shade and therefore extremely cold. Observations by the "Clementine" spacecraft suggest that one such crater may indeed contain a layer of ice.
|
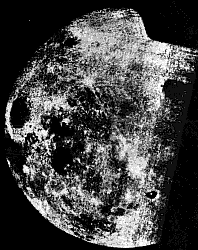
In the Space AgeFrom the beginning of spaceflight, the Moon was a prime target, but this chapter in space exploration is too long to be covered here in any detail. The first spacecraft to reach the Moon were Luna 1, 2 and 3 of the Soviet Union, in 1959. Of these, Luna 3 rounded the Moon, took photographs of the far side which is not seen from Earth, and later scanned and transmitted those images (on the right); unfortunately, their quality was poor. In the decade that followed, 19 other Soviet missions were aimed at the Moon.In 1970 a Soviet spacecraft landed and returned a rock sample, and later that year a remotely controlled "Lunokhod" vehicle was landed, exploring its surroundings for nearly a year. Other sample returns and Lunokhods followed, the series ending in 1976. However, failures marked tests of a large rocket developed for human Moon flights, ending any plans of manned lunar exploration by the Soviet Union. Early attempts by the US to send unmanned spacecraft to the Moon (1958-64) either failed or returned scanty data. In July 1964, however, Ranger 7 returned clear TV pictures of its impact on the Moon, as did Rangers 8 and 9. Of the 7 "soft landers" in the "Surveyor" series (1966-8), 5 performed well and sent back data and pictures. In November 1969, after Apollo 12 landed 500 feet (160 meters) from the "Surveyor 3" lander, astronauts retrieved its camera and brought if back to Earth. In addition to the Surveyor project, 5 lunar orbiters photographed the Moon and helped produce accurate maps of its surface.
The Apollo missions followed, with Apollo 8 rounding the Moon in 1968 and Apollo 11 finally landing there, on July 20, 1969. Five other lunar landings followed, the last of them in December 1972. Only Apollo 13 failed to land, its crew members narrowly escaping with their lives after an explosion aboard their craft on the way to the Moon.
Achievements of "Project Apollo."
|
|
No humans have visited the Moon from 1972 until now, but some orbital missions have studied the Moon's magnetic field as well as X-ray and gamma-ray emissions, from which some variations of the surface composition could be inferred. The Moon was found to have no global magnetic field like the Earth, but its surface was weakly magnetized in some patches. Molten rock can become permanently magnetized if it solidifies in the presence of an external magnetic field, suggesting that in some ancient era the Moon, like Earth now, had a molten metallic core in which electric currents generated a magnetic field. Somewhat similar observations were made near Mars in 1998-2000. Some excitement was caused by indications from the Lunar Prospector spacecraft, which suggested that ice may exist on the moon, inside a deep crater near the Moon's south pole. A possible explanation was that some time in the past (perhaps long ago) a comet had crashed into the Moon, and comets contain considerable amounts of water ice. The energy of the impact, turned into heat, would of course evaporate the ice. However, some of the water vapor would form a temporary atmosphere around the Moon, and might condense again to ice in very cold locations, like craters near the pole, which are permanently shaded from sunlight. At the end of its mission, on July 31, 1999, Lunar Prospector was therefore steered to deliberately crash inside the crater. It was hoped the impact might create (briefly) a cloud of water vapor, which could be observed from Earth, but none was detected. There is little doubt that the future will see further lunar exploration, though a "lunar base" is probably far off. Astronomical and other observations can readily be made from Earth orbit, and providing life support on the Moon is not easy. Such a base will probably become attractive only after ways are developed for utilizing local lunar materials for construction and for fuel.
|
Exploring FurtherEntire books about "Project Apollo" can be found of the web. Some good ones:
A site about impact craters on Earth.
|
#############################################
(concerning the "Palimpsest Craters" on Jupiter's moons)
|
Palimpsest is the word On my tongue and my mind When on waveswept expanses Of seashore I find Angular outlines Traced in the sand Where castles and citadels Once used to stand. Now erased by the tides They resemble, indeed, Those ancient craters That mark Ganymede Which sagged to the surface Completely depressed Until just their outline remained: Palimpsest. My mind's own parchment Like the sands of the shore Is erased and reused It is pristine no more. Elisha ben Avuyah, it's written, Once said He who studies God's law While still a young lad Has a mind like fresh parchment At its cleanest and best But in old age the mind Is a mere Palimpsest. DPS 1982
|
|
Note: The ancient Greeks and Romans did not have paper: their books were hand-written on parchment--specially treated animal skin, forming thin hard sheets. Parchment was expensive, and therefore when a book was no longer of great interest, the letters on its parchment were sometimes carefully scraped away with a knife and the pages re-used. Such a clean-scraped parchment--usable, but no longer as good as new--was known as a palimpsest. The quote from Elisha be Avuyah, named among ancient Jewish sages though himself an apostate, is in the Mishnah, Sayings of the Fathers, VI, v. 25.
|

(4c) The Brightest Moon of the CenturySince moonshine is really reflected sunlight, the full Moon is on the average slightly brighter in mid-winter, when Earth is closest to the Sun. In addition, the distance of the full Moon also varies, due to the ellipticity ("eccentricity") of the Moon's orbit. On 22 December, 1999, the two effects combined to produce the brightest full Moon of the century. On the preceding day, NASA released the following "Educational Update": ***********************************
On December 21st. 1866 the Lakota Sioux took advantage of this combination of occurrences and staged a devastating retaliatory ambush on soldiers in the Wyoming Territory. In laymen's terms it will be a super bright full moon, much more than the usual AND it hasn't happened this way for 133 years! Our ancestors 133 years ago saw this. Our descendants 100 or so years from now will see this again. Remember this will happen December 22, 1999.
***********************************
Additional Exploring"Astronomy Picture of the Day" devoted two sites to the above phenomenon:
On 12.22.1999 it showed the difference in the apparent size of the Moon, |
###########################
|
Any location on Earth is described by two numbers--its latitude and its longitude. If a pilot or a ship's captain wants to specify position on a map, these are the "coordinates" they would use. Actually, these are two angles, measured in degrees, "minutes of arc" and "seconds of arc." These are denoted by the symbols (°,',") e.g. 35° 43' 9" means an angle of 35 degrees, 43 minutes and 9 seconds (do not confuse this with the notation (', ") for feet and inches!). A degree contains 60 minutes of arc and a minute contains 60 seconds of arc--and you may omit the words "of arc" where the context makes it absolutely clear that these are not units of time. Calculations often represent angles by small letters of the Greek alphabet, and that way latitude will be represented by l (lambda, Greek L), and longitude by f (phi, Greek F). Here is how they are defined.
Latitude |
| Imagine the Earth was a transparent sphere (actually the shape is slightly oval; because of the Earth's rotation, its equator bulges out a little). Through the transparent Earth (drawing) we can see its equatorial plane, and its middle the point is O, the center of the Earth. To specify the latitude of some point P on the surface, draw the radius OP to that point. Then the elevation angle of that point above the equator is its latitude l--northern latitude if north of the equator, southern (or negative) latitude if south of it.
|
Good question. We must use the angle which completes it to 90 degrees, the one between the given line and one perpendicular to the plane. Here that would be the angle (90°-l) between OP and the Earth's axis, known as the co-latitude of P.] |
| On a globe of the Earth, lines of latitude are circles of different size. The longest is the equator, whose latitude is zero, while at the poles--at latitudes 90° north and 90° south (or -90°) the circles shrink to a point.
LongitudeOn the globe, lines of constant longitude ("meridians") extend from pole to pole, like the segment boundaries on a peeled orange.
|
|
Every meridian must cross the equator. Since the equator is a circle, we can divide it--like any circle--into 360 degrees, and the longitude f of a point is then the marked value of that division where its meridian meets the equator.
|
|
|
What that value is depends of course on where we begin to count--on where zero longitude is. For historical reasons, the meridian passing the old Royal Astronomical Observatory in Greenwich, England, is the one chosen as zero longitude. Located at the eastern edge of London, the British capital, the observatory is now a public museum and a brass band stretching across its yard marks the "prime meridian." Tourists often get photographed as they straddle it--one foot in the eastern hemisphere of the Earth, the other in the western hemisphere.
Local Time (LT) and Time ZonesLongitudes are measured from zero to 180° east and 180° west (or -180°), and both 180-degree longitudes share the same line, in the middle of the Pacific Ocean.As the Earth rotates around its axis, at any moment one line of longitude--"the noon meridian"--faces the Sun, and at that moment, it will be noon everywhere on it. After 24 hours the Earth has undergone a full rotation with respect to the Sun, and the same meridian again faces noon. Thus each hour the Earth rotates by 360/24 = 15 degrees. When at your location the time is 12 noon, 15° to the east the time is 1 p.m., for that is the meridian which faced the Sun an hour ago. On the other hand, 15° to the west the time is 11 a.m., for in an hour's time, that meridian will face the Sun and experience noon. In the middle of the 19th century, each community across the US defined in this manner its own local time, by which the Sun, on the average, reached the farthest point from the horizon (for that day) at 12 oclock. However, travelers crossing the US by train had to re-adjust their watches at every city, and long distance telegraph operators had to coordinate their times. This confusion led railroad companies to adopt time zones, broad strips (about 15° wide) which observed the same local time, differing by 1 hour from neighboring zones, and the system was adopted by the nation as a whole. The continental US has 4 main time zones--eastern, central, mountain and western, plus several more for Alaska, the Aleut islands and Hawaii. Canadian provinces east of Maine observe Atlantic time; you may find those zones outlined in your telephone book, on the map giving area codes. Other countries of the world have their own time zones; only Saudi Arabia uses local times, because of religious considerations. In addition, the clock is generally shifted one hour forward between April and October. This "daylight saving time" allows people to take advantage of earlier sunrises, without shifting their working hours. By rising earlier and retiring sooner, you make better use of the sunlight of the early morning, and you can enjoy sunlight one hour longer in late afternoon.
The Date Line and Universal Time (UT)Suppose it is noon where you are and you proceed west--and suppose you could travel instantly to wherever you wanted.Fifteen degrees to the west the time is 11 a.m., 30 degrees to the west, 10 a.m., 45 degrees--9 a.m. and so on. Keeping this up, 180 degrees away one should reach midnight, and still further west, it is the previous day. This way, by the time we have covered 360 degrees and have come back to where we are, the time should be noon again--yesterday noon. Hey--wait a minute! You cannot travel from today to the same time yesterday! We got into trouble because longitude determines only the hour of the day--not the date, which is determined separately. To avoid the sort of problem encountered above, the international date line has been established--most of it following the 180th meridian--where by common agreement, whenever we cross it the date advances one day (going west) or goes back one day (going east). That line passes the Bering Strait between Alaska and Siberia, which thus have different dates, but for most of its course it runs in mid-ocean and does not inconvenience any local time keeping. Astronomers, astronauts and people dealing with satellite data may need a time schedule which is the same everywhere, not tied to a locality or time zone. The Greenwich mean time, the astronomical time at Greenwich (averaged over the year) is generally used here. It is sometimes called Universal Time (UT).
Right Ascension and DeclinationThe globe of the heavens resembles the globe of the Earth, and positions on it are marked in a similar way, by a network of meridians stretching from pole to pole and of lines of latitude perpendicular to them, circling the sky. To study some particular galaxy, an astronomer directes the telescope to its coordinates.On Earth, the equator is divided into 360 degrees, with the zero meridian passing Greenwich and with the longitude angle f measured east or west of Greenwich, depending on where the corresponding meridian meets the equator. In the sky, the equator is also divided into 360 degrees, but the count begins at one of the two points where the equator cuts the ecliptic--the one which the Sun reaches around March 21. It is called the vernal equinox ("vernal" means related to spring) or sometimes the first point in Aries, because in ancient times, when first observed by the Greeks, it was in the zodiac constellation of Aries, the lamb. It has since then moved, as is discussed in the later section on precession. The celestial globe, however, uses terms and notations which differ somewhat from those of the globe of the Earth. Meridians are marked by the angle a (alpha, Greek A), called right ascension, not longitude. It is measured from the vernal equinox, but only eastward, and instead of going from 0 to 360 degrees, it is specified in hours and other divisions of time, each hour equal to 15 degrees. Similarly, where on Earth latitude goes from 90° north to 90° south (or -90°), astronomers prefer the co-latitude, the angle from the polar axis,equal to 0° at the north pole, 90° on the equator, and 180° at the south pole. It is called declination and is denoted by the letter d (delta, Greek small D). The two angles (a,d), used in specifying (for instance) the position of a star are jointly called its celestial coordinates. The next section tells how the stars, the Sun and accurate clocks allowed sailors to find their latitude and longitude.
|
" Astronomy without a telescope," a very extensive site on a somewhat higher level than this exposition. It covers coordinates, zodiac, star maps, precession (sect. #7 below) and much more.
Next Stop: #5a. Navigation
########################
|
I must go down to the sea again To the lonely sea and sky And all I ask is a tall ship And a star to steer her by Sea Fever by John Masefield
|
|
How does a captain determine a ship's position in mid-ocean? In our space age, this is easily done, by using the GPS system of satellites--the Global Positioning System. That network of 24 satellites constantly broadcasts its positions, and small hand-held receivers exist which convert those signals into positions accurate within 15 meters or about 50 feet. Before the space age, however, it was not as easy. One had to use the Sun and the stars.
|
Finding latitude with the Pole StarImagine yourself standing at night at point P on Earth and observing the pole star (or better, the position of the north celestial pole, near that star), at an elevation angle h above the horizon.The angle between the direction of the pole and the zenith is then (90°-h) degrees. If you continue the line from zenith downwards (see drawing) it reaches the center of the Earth, and the angle beween it and the Earth's axis is also (90°-h). Therefore (as the drawing shows) h is also your latitude.
|
|
Finding latitude with the noontime SunIf you are sailing a ship in mid-ocean, you can get the same information from the noontime Sun--probably more accurately, since at night you might not see the horizon very well.Noon is when the Sun reaches the highest point in its journey across the sky. It then crosses the north-south direction--in the northern hemisphere, usually south of the observer. Because the axis of the Earth is inclined by an angle e = 23.5° to a line perpendicular to the ecliptic, the height of that point above the horizon depends on the season. Suppose you are at point P. We examine 3 possibilities:
|
| (1) Suppose the date is the winter solstice, around December 21, when the north pole is inclined away from the Sun. To find your latitude l you measure the angle a between the direction of the noontime Sun and the zenith.
Look at the drawing and imagine you could rotate
|
|
(2) Half a year later, at the summer solstice (June 21), the north pole is inclined towards the Sun, not away from it, and now (if l is larger than e)
|
|
| (3) Finally, suppose you are at equinox, around March 21 or September 21. The inclination of the Earth's axis is now out of the plane of the drawing--away from the paper, if this were a picture in a book. The direction to the Sun is in the plane of the equator, and we get
|
|
Thus at least at those dates, seafarers could tell what their latitude was by measuring the position of the noontime Sun. For any other date, navigation tables exist that give the proper angle (smaller than 23.5 degrees) which must be added or subtracted. They also provide formulas for deriving the height of the noontime Sun from observations made at other times. As with the pole star, rather than measuring the angle a from the zenith--which is not marked in the sky!--it is simpler to measure the angle (90°-a) from the horizon, which at sea is usually sharply defined. Such observations, known as "shooting the Sun," are done with an instrument known as the sextant. It has a sliding scale covering 1/6 of a circle (hence the name) and an attached pivoted mirror, providing a split view: by moving the scale, the sea-officer brings Sun and horizon simultaneously into view and then reads off the angle between them.
LongitudeIn the age of the great navigators--of Columbus, Magellan, Drake, Frobisher, Bering and others--finding your latitude was the easy part. Captains knew how to use the noontime Sun, and before the sextant was invented, a less precise instrument known as the cross-staff was widely used.Longitude was a much harder nut to crack. In principle, all one needs is an accurate clock, set to Greenwich time. When the Sun "passes the meridian" at noon, we only need to check the clock: if Greenwich time is 3 p.m., we know that 3 hours ago it was noon at Greenwich and we are therefore at longitude 15° x 3 = 45 degrees west. However, accurate clocks require a fairly sophisticated technology. Pendulum clocks can keep time quite accurately on firm land, but the pitching and rolling of a ship makes them quite unsuitable for sea duty. Non-pendulum clocks--e.g. wristwatches, before they became electronic--use a balance wheel, a small flywheel rotating back and forth through a small angle. A flat spiral spring is wrapped around its axis and it always brings the wheel back to its original position. The period of each back-and-forth oscillation is then only determined by the strength of the spring and the mass of the wheel, and it can replace the swing of the pendulum in controlling the motion of the clock's hands. Gravity plays no role here, and motions of the ship also have very little effect; as discussed in a later section, a vaguely similar method was used in 1973 for "weighing" astronauts in the weightless environment of a space station. For navigation, however, such a clock must be very accurate, which is not easy to achieve: friction must be minimal, and so must changes in the dimensions of the balance wheel and properties of the spring due to changing temperature and other factors. In the 17th and 18th century, when the navies of Britain, Spain, France and Holland all tried to dominate the seas, the "problem of longitude" assumed great strategic importance and occupied some of the best scientific minds. In 1714 Britain announced a prize of 20,000 pounds--a huge sum in those days--for a reliable solution, and John Harrison, a British clockmaker, spent decades trying to achieve it. His first two "chronometers," of 1735 and 1739, though accurate, were bulky and delicate pieces of machinery; they have been restored and are ticking away on public display, at the Royal Astronomical Observatory in Greenwich. Only his 4th instrument, tested in 1761, proved satisfactory, and it took some additional years before he received his prize. An extensive and delightful web site on the story of the "longitude problem," by Jonathan Medwin, can be reached here. Another recommended source is the book Longitude by Dava Sobel. |
Next Stop: #5b. The Cross-Staff (and how to build your own)