|
You will also note some differences: "Shabatu" comes before "Tebetu", whereas in today's Jewish calendar, Tevet comes first, Shvat later. In the three names containing the letter "m" it was replaced in the Jewish calendar by "v" (or "w"), "Du'uzu" is now Tamuz, the name of the god of spring (later known as Adonis), and "Arach-samna" has become "Marcheshvan" or "Cheshvan" for short.
The Start of the Year
When does the Jewish year begin? Tradition has been somewhat ambiguous here. Rosh Hashanah, the official Jewish New Year's Day, is celebrated on the 1st day of Tishrey--but the Bible never calls it "Rosh Hashanah," it is always "Yom Hazikaron," the day of remembrance. And in the biblical chronology, this is not (as you might think) the first day of the first month--no, it is the first day of the seventh month, counting Nissan as the first.
In fact, none of these ancient names is in the Bible--all of them were handed down strictly by oral tradition. The Bible only uses numbers--first month, second month and so on--maybe to make sure that the month of Passover was always the first.
According to the scriptures, this renumbering was done in memory of the exodus from Egypt. At the beginning of chapter 12 in the book of Exodus you will find:
"This month shall be unto you the beginning of months; it shall be the first month of the year to you."
Well, maybe. But it is interesting that the Babylonian calendar had the same ambiguity. There too, two months served as pivots--Nissan and Tishrey. Maybe one was the start of the religious year, one of the tax year--since in Nissan the harvest just starts and in Tishrey the crops are all in--maybe they date to different periods or localities, maybe the year was divided into two 6-month sections. One can only speculate.
Keeping up with both Sun and Moon
If the Jewish calendar only followed the Moon, it would get quickly out of step with the seasons, which follow the cycle of the Sun--the holidays would migrate and you might get Passover in the fall, Rosh Hashanah in the spring, Chanukkah in mid-summer. That is what happens in the Moslem calendar, which only follows the moon.
Consider the month of Ramadan, when observant Moslems fast from sunrise to sundown. Ramadan this year was in early winter--the best time, because days are short, nights are long, your fasts are short too and you do not get too thirsty from heat. But wait 15 years! Then Ramadan will have migrated to mid-summer, when days are at their longest, the heat makes you quite thirsty (especially in countries like Arabia and Egypt), and fasting all day long is a much greater ordeal.
But the ancient Babylonians found a way to keep up with both the moon and the sun. Their priests were excellent astronomers--helped, no doubt, by the clear skies in a country perched at the edge of the desert.
(By the way, the Jewish Talmudic sage Mar Shmuel, who lived in Babylonia in the 3rd century, was also experienced in astronomy. He used to say "I am familiar with the pathways of the heavens as I am familiar with the pathways of [my home town] Nehard'a--except for the comet-star, I don't know what it is.")
By the 9th century BCE, after centuries of observations, Babylonian astronomers concluded that in a cycle of 19 years of 12 lunar months each, if you added 7 more months, you returned almost exactly to the same season.
Today this system is known as the Metonic cycle, because the Greek astronomer Meton introduced it in Athens in the year 432 BCE. However, the Babylonians already knew this at least 400 years earlier. The Chinese also have used this system--and the Jewish calendar does the same.
So how do you know which year has a seond month of Adar? Simple: in every 19-year cycle, years 3, 6, 8, 11, 14, 17 and 19 are leap years. This 19-year sequence is known as the "machzor," meaning "cycle" in Hebrew. In the general calendar, we now have Y2K, a special "millenium" year--but I still remember in 1940 or 1941, when I was 9 years old, the teacher told us that the current year 5700 was special, because it marked exactly 300 cycles since the creation of the world, according to the Jewish calendar.
So--3 times 19 is 57, 300 times 19 is 5700, and the year 5757 would complete 303 cycles. We are now in the year 5760, 3 years into cycle number 304, so by the rule assigning extra months to years 3, 6, 8, 11, 14, 17 and 19, it is a leap year. And the additional month is Adar, because it is the 12th and last month. The ancient Babylonians also added a 2nd Adaru--though sometimes they would add instead a second "Ululu" just before the day which became Rosh Hashanah.
One could go on and on. The Babylonians did not have a sabbath--but they preferred not to work on the 7th, 14th, 21st and 28th day of the month, because they thought those were unlucky days. Is there a connection? Who knows!
Accuracy
I have not yet touched at all our civil calendar, by which this February of the year 2000 is a very special leap month, instituted to fine-tune the calendar. Or that yesterday's date, February 11, was the day George Washington was born--in 1732, on February 11, old style. Then in 1751 the calendar was advanced 11 days, to make up for 17 centuries when this fine-tuning was not yet known, so now America celebrates Washington's birthday on February 22nd.
The Jewish calendar is much more accurate than the old-style calendar used when Washington was born. Still, in the 3500 years or so since the exodus from Egypt, it has slipped by about two weeks. According to the Bible, the exodus took place at the spring equinox, around March 21, and now Passover is about 2 weeks later. However, as long as one uses a calendar that tries to keep up with both the Sun and the Moon, there is nothing one can do about it--except maybe, wait a few thousand years more and then omit an entire leap month.
|

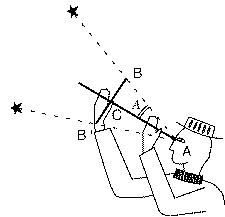 To measure the angle between two stars, the astronomer would place the staff just below one eye (drawing) and slide the cross-piece up and down. The cross-piece would have a pair of nails sticking out perpendicular to the drawing at symmetric locations such as B and B' (often several pairs of nails). The astronomer would slide the cross-piece up and down, until nail B one of the stars and nail B' the other.
To measure the angle between two stars, the astronomer would place the staff just below one eye (drawing) and slide the cross-piece up and down. The cross-piece would have a pair of nails sticking out perpendicular to the drawing at symmetric locations such as B and B' (often several pairs of nails). The astronomer would slide the cross-piece up and down, until nail B one of the stars and nail B' the other.  You will need:
You will need:

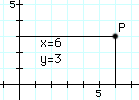
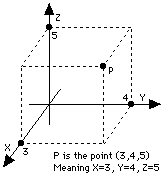 This works well on a flat sheet of paper, but the real world is 3-dimensional and sometimes it is necessary to label points in 3-dimensional space. The cartesian (x,y) labeling can be extended to 3 dimensions by adding a third coordinate z. If (x,y) is a point on the sheet, then the point (x,y,z) in space is reached by moving to (x,y) and then rising a distance z above the paper (points below it have negative z).
This works well on a flat sheet of paper, but the real world is 3-dimensional and sometimes it is necessary to label points in 3-dimensional space. The cartesian (x,y) labeling can be extended to 3 dimensions by adding a third coordinate z. If (x,y) is a point on the sheet, then the point (x,y,z) in space is reached by moving to (x,y) and then rising a distance z above the paper (points below it have negative z). 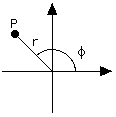 Cartesian c oordinates (x,y) are not the only way of labeling a point P on a flat plane by a pair of numbers. Other ways exist, and they can be more useful in special situations.
Cartesian c oordinates (x,y) are not the only way of labeling a point P on a flat plane by a pair of numbers. Other ways exist, and they can be more useful in special situations. 





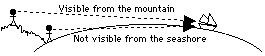

 Imagine you were standing at an elevation of h meters above the ocean and looking out across the water. What is the distance D to the horizon? It can be calculated, if you know the radius R of the Earth.
Imagine you were standing at an elevation of h meters above the ocean and looking out across the water. What is the distance D to the horizon? It can be calculated, if you know the radius R of the Earth.


 Also, the Earth's shadow has only approximately the width of 2r. It would have very nearly a width of 2r if the Sun were a point-like light source (exactly that width if it were infinitely far away). Actually, however, the Sun is large enough to appear as a disk which covers about half a degree of the sky. As a result, the Earth's shadow is not a cylinder but a gradually narrowing cone, and at the Moon's distance it is already about 25% narrower than 2r.
Also, the Earth's shadow has only approximately the width of 2r. It would have very nearly a width of 2r if the Sun were a point-like light source (exactly that width if it were infinitely far away). Actually, however, the Sun is large enough to appear as a disk which covers about half a degree of the sky. As a result, the Earth's shadow is not a cylinder but a gradually narrowing cone, and at the Moon's distance it is already about 25% narrower than 2r.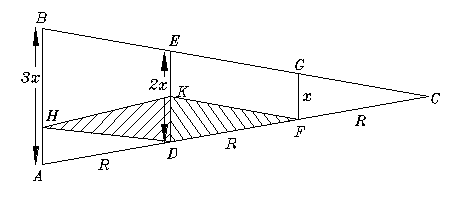

 One reason an excessive value was obtained is that the Moon was assumed to be overhead at A or B. Actually, it is likely to be at some significant angle to the overhead direction, the "zenith" (see drawing).
One reason an excessive value was obtained is that the Moon was assumed to be overhead at A or B. Actually, it is likely to be at some significant angle to the overhead direction, the "zenith" (see drawing). 