Energie
L'énergie peut être grossièrement définie comme tout ce qui peut faire fonctionner une machine. Les formes d'énergie qui actionnent nos machines sont habituellement l'électricité ou la chaleur ; la lumière en est une autre forme, qui convertie en électricité par les panneaux solaires actionne la plupart des satellites.
La pesanteur peut également être source d'énergie. Les rouages des horloges de première génération tournaient grâce à des poids, descendant graduellement de la base de l'horloge, et devaient être régulièrement remontés , sous peine d'arrêt de l'horloge. Thomas Jefferson, dans sa maison de Virginie proche de Charlottesville, possédait une horloge dont les poids (installés à côté de la salle) étaient des boulets de canon attachés à une corde. Pour donner un laps de temps de sept jours à l'horloge, un trou avait été découpé dans le plancher, leur permettant de descendre jusqu'au sous-sol.
Quand un poids, ou un boulet de canon, est relevé contre la force de la pesanteur, il acquiert de l'énergie potentielle , énergie résultant de la position, et proportionnelle à la hauteur à laquelle l'objet a été monté . Si le poids est lâché, il perd de la hauteur et donc de l'énergie potentielle, mais il gagne en
énergie cinétique, celle qui est due à la vitesse du mouvement. L'énergie cinétique peut à son tour être reconvertie en énergie potentielle, comme c' est le cas pour les obstacles pour " rollers " qui passent au fond d'un creux puis entament une montée.
Un échange semblable se produit si une pierre est jetée vers le haut avec une certaine vitesse v . Si sa masse est m (la masse sera définie plus tard, mais c' est quelque chose qui est lié au poids), on peut démontrer que son énergie cinétique est
1/2 mv2
Pendant l'élévation, v et l'énergie cinétique diminuent, mais cela est assorti d'une croissance d'énergie potentielle :
h m g
avec h : hauteur en mètres et g : une constante mesurant la force de la pesanteur. Si
m est exprimé en kilogrammes, h en mètres et
v en mètres par - seconde (s'écrit : m/sec ; la vitesse d'un marcheur est de 1-2m /sec), g vaut environ 9.81.
De la somme des deux résulte l'énergie totale E qui reste constante:
E = 1/2
mv2 + h m g = constante
Quand la pierre s'élève, la partie cinétique de son énergie diminue , puis est nulle au point le plus élevé, quand pendant un bref instant v = 0. En descendant, les modifications sont inverses. Nous reviendrons ultérieurement sur cette formule et sur le concept d'énergie.
Pour un satellite de masse m , tournant autour de la terre, (ou pour une planète autour du soleil) il y a une formule semblable :
E = 1/2 mv2 – k m/r = constante
Ici k est une autre constante, en fait, dépendante de
g, puisque toutes deux reflètent la force de la pesanteur de la terre (la valeur exacte est k = g R2, où
R est le rayon de la terre, en mètres). Ne vous laissez pas surprendre par le signe moins : si le satellite s'élève, r augmente, donc k m/r diminue, mais –k m/r augmente, il est moins négatif que près de la terre. Cette équation montre donc pourquoi la vitesse du satellite diminue pendant qu'il s'éloigne et augmente pendant qu'il se rapproche.
Si le satellite a juste assez de vitesse pour échapper complètement à la pesanteur de la terre (C' est la "vitesse d'évasion" V ), il s'éloigne assez de la terre, pour que k m/r ) pour que r tende vers zéro, et son énergie cinétique est également épuisée, puisque v= 0. Comme la somme E reste toujours identique, cela montre que pour une sonde spatiale échappant juste à la pesanteur de la terre,
E=0. On a donc :
V2 = 2k/R = 2 g R
Avec g = 9.81 et R =6 371 000 mètres , on trouve V à environ 11200 m /sec.
l'Anomalie Moyenne
nous avons déjà indiqué qu'un troisième élément orbital était nécessaire pour fixer la
localisation du satellite sur son orbite. Puisque celle ci est une ellipse, on a :
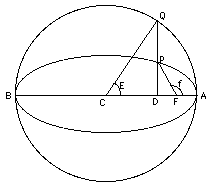
r = a(1 - e2)/(1 + e cos f)
Chaque valeur de l'angle f , appelée "anomalie vraie", indique la position le long de l'orbite. On peut donc l'utiliser comme troisième élément orbital.
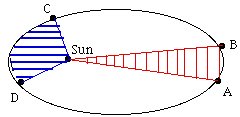
L'anomalie vraie f varie périodiquement autour de l'orbite, rapidement près du périgée et lentement près de l'apogée. La seconde loi de Kepler indique complètement cette variation et il devrait suffire d'obtenir une formule des variations de f en fonction du temps t.
Malheureusement, aucune solution simple n'existe pour exprimer cette formule.
|