Vecteurs : Prolongements des nombresLe concept des nombres s'est développé très graduellement. Au début il y avait les nombres entiers positifs -- 1,2,3... (et non zéro, un apport beaucoup plus récent) qui servait à décrire des objets que l'on peut compter, tels que des moutons, des jours, des membres de tribu, etc... Le concept de nombres négatifs peut être conçu comme une prolongation de la soustraction, peut-être celle de l'argent, vos dettes étant des richesses négatives, à l'encre rouge dans le gros cahier. Les objets qui peuvent être divisés, les terrains , par exemple, sont à l'origine des fractions. Par la suite, vers 500 ans BC, l'école de Pythagore a démontré que la racine carrée de 2 ne peut jamais être mise en fraction : Cela n'avait aucun sens pour eux, et donc nous disons toujours que ce sont des nombres "irrationnels". Avec les nombres entiers, les fractions et les irrationnels on peut décrire tout ce qui a une grandeur, une magnitude. Mais comment décrire une vitesse, qui présente à la fois une grandeur et une direction ? Un vecteur, voilà ce qui est nécessaire ! Addition de vecteursLes vitesses peuvent être ajoutées. Supposez qu'un avion vole à 200 M/H (ou si vous préférez, kilomètres par heure) avec un vent arrière de 100 M/H. Quelle distance parcourt - il par rapport à la terre ? Facile : Quand il a avancé de 200 milles, le vent l'a poussé en plus de 100 milles, et la réponse est Graphiquement, chaque distance sur terre ,ou chaque vitesse, peut être
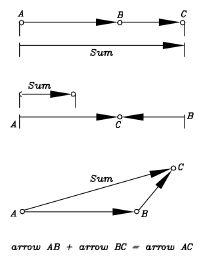
représenté par une flèche qui donne la direction, et dont la
longueur donne la valeur. Par exemple, une flèche AB de 200 millimètres de
long pour le mouvement propre de l'avion et encore une autre, BC ,de 100
millimètres de long, dans la même direction, pour le vent. Pour ajouter
les vitesses, mettez-les bout à bout, comme ici dans en haut de la
figure . et "l'addition des flèches" (figure du milieu) le confirme. Supposons maintenant que le pilote se dirige vers l'est, mais qu'il y a un vent vers le nord-est, de 100 M/H : dans quelle direction l'avion se déplace-t-il, et à quelle vitesse ? Ici, l'intuition ne suffit pas, mais "l'addition des flèches" permet de résoudre le problème.(figure du bas, non à l' échelle). La règle générale est que les vitesses combinées déportent l'avion au même point que si le premier mouvement, puis l'autre, agissaient successivement pendant le même temps, une heure. Comme prévisible, la direction est quelque part entre l'est et le nord. Tous les vecteurs peuvent ainsi être ajoutés, comme les
flèches, de la tête à la queue. Mais il existe une autre méthode , souvent
plus facile à employer, qui est décrite ci dessous.
Utilisations des vecteurs composants(a) Addition de plusieurs vecteursSupposons qu'il faille ajouter 10 vecteurs (eh, oui, ces situations existent) Selon le procédé qui vient d'être décrit, on ajouterait les deux premiers vecteurs bout à bout, puis un troisième, puis un quatrième. Travail pénible!Une façon plus rapide est de choisir deux directions perpendiculaires: en choisissant des coordonnées cartésiennes, une direction sera appelée la direction de "x" et l'autre celle de "y". Décomposons chaque vecteur V en "composants de x": Vx ,et en "composants de y": Vy, selon celle de y. On obtient maintenant non pas 10, mais 20 vecteurs qui doivent être ajoutés, mais le travail est beaucoup plus simple. Parmi ces vecteurs, 10 sont alignés dans la direction de x, mais les vecteurs de même direction s'ajoutent comme des nombres ordinaires (comme les vitesses de vent "dans le nez" ou "arrière" de l'avion dans l'exemple précédent). Il en va de même pour les 10 vecteurs alignés dans la direction y. Le problème se réduit maintenant à deux séries d'additions ordinaires, ou de soustractions (un vecteur en direction opposée ayant un signe négatif ). Ce n'est que pour la dernière étape, la combinaison des deux totaux généraux dans les directions x and y, qu'il est besoin d'une addition de type vectorielle.
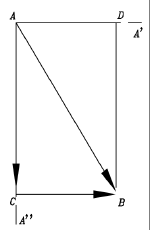
(b) Calcul d'une somme "résultante" de vecteursL'addition des vecteurs, de leurs origines à leurs terminaison, permet de construire leur somme graphiquement. Gr'ce aux divers composants, on peut calculer celle ci.Dans l'exemple de l'addition des vecteurs, un avion vole vers l'est à 200 M/H (sa vitesse anémométrique, sa vitesse mesurée relativement à l'air), et il y a un vent de 100 M/H vers le nord-est. Le triangle d'addition des vecteurs de cet exemple est en bas de la première figure de cette section. Posons x la direction vers l'est, et y celle vers le nord. les composants de la vitesse (x, y) sont alors, en M/H :
Ceci donne la vitesse résultante, V. Par le théorème de Pythagore,
et la valeur de V est approximativement de 280 M/H, alors que l'angle aigu du point A de la figure (nous l'appellerons aussi A) correspond à
D'ou l'on tire A = environ 16.25 °. (c) Le plan inclinéRevenons à #39; l'expérience de Galilée. Soit une pente lisse inclinée d'un angle s (dessin) et dessus un bloc bien graissé, prêt à glisser vers le bas (Galilée avait utilisé une boule "roulante", qui facilitait l'expérience mais perturbait le résultat, puisque l'énergie cinétique est alors partagée entre les mouvements de glissement et de rotation). A quelle vitesse glisse le bloc, si le frottement est négligeable?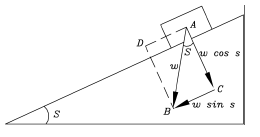 La force qu'exerce la pesanteur sur le bloc porte un nom, le poids W,dirigée directement vers le bas. Ce n'est pas la direction dans laquelle le bloc accélère. Mais ce vecteur AB peut également être décomposé en deux forces mutuellement perpendiculaires :
|