Un raffinamento della Prima Legge
La prima legge di Keplero era espressa così:
"L'orbita di un pianeta è un'ellisse, di cui il Sole occupa uno dei fuochi"
In realtà questo non è del tutto preciso. Immaginiamo che magicamente il pianeta diventi sempre più pesante, e che il Sole diventi sempre più leggero. A un certo momento entrambi avranno la stessa massa: come potremo allora dire qual'è dei due che orbita intorno all'altro?
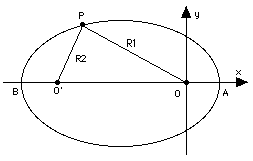
Per essere completamente accurata, la prima legge avrebbe dovuto porre il fuoco dell'ellisse orbitale nel centro di gravità del sistema pianeta-Sole. (Il centro di gravità sarà definito più avanti, ma, intuitivamente, se le masse sono molto diverse tra loro, come nel caso di un pianeta e del Sole, il centro di gravità si trova molto vicino al centro del corpo più pesante). Poiché il Sole è molto più pesante di Marte, l'effetto sull'orbita di Marte, che Keplero aveva studiato, era troppo piccolo perché fosse da lui notato. Tuttavia anche il Sole si muove come conseguenza del moto dei pianeti, e i movimenti di questo tipo sono diventati uno strumento molto importante per cercare altri pianeti fuori del nostro Sistema Solare.
Un pianeta delle dimensioni della Terra in orbita attorno a una stella lontana sarebbe troppo debole per essere rivelato da un telescopio sulla Terra, specialmente a causa del bagliore luminoso del suo sole, la stella stessa. Tuttavia, mentre il pianeta percorre la sua orbita, anche la sua stella si muove lungo un'orbita speculare attorno al comune centro di gravità. Si tratta di un'orbita molto più piccola e di un moto molto più lento, poiché il centro di gravità è molto vicino al centro della stella (nel sistema Terra-Sole, si trova all'interno del Sole), tuttavia l'effetto può essere rivelato da piccole variazioni della luce della stella.
Recentemente sono stati trovati, con questo metodo, alcuni pianeti, ma quasi tutti hanno le dimensioni di Giove e nessuno di essi sembra adatto ad ospitare la vita. La ricerca, comunque, prosegue, e dati aggiornati in proposito (oltre a molte altre notizie) si possono trovare sul sito "Planet Quest" ("Ricerca dei pianeti"), un sito Web del Jet Propulsion Lab (JPL) della NASA. Una scoperta abbastanza recente (15 aprile 1999) è stata quella del sistema di ipsilon Andromeda che sembra comprendere almeno tre pianeti. Per un'altra recente scoperta riguardante un pianeta al di fuori del Sistema Solare, si può fare clic qui.
Gli oggetti nel Sistema Solare si possono muovere anche lungo altri tipi di sezioni coniche, come parabole e iperboli, le cui equazioni rassomigliano a quella dell'ellisse, ma hanno e uguale a 1 o anche maggiore. Strettamente parlando, queste orbite non hanno un "semiasse maggiore", poiché non hanno dimensioni limitate come le ellissi, ma si estendono fino all'infinito. L'equazione viene allora scritta
r = p/(1 + e cos φ)
che non presenta problemi quando e = 1. Tali corpi non sono legati al Sole, ma sono liberi di abbandonarlo. Il denominatore nell'equazione della traiettoria diventa zero per alcuni valori di φ, rendendo r infinito, e, quando per un oggetto di questo tipo si raggiungono tali valori, esso si allontana sempre di più, senza limiti. In genere le comete hanno un'eccentricità e prossima a 1, suggerendo così che provengono da regioni molto remote del Sistema Solare. La sonda spaziale Voyager 2 ha un'orbita con e > 1 ed è stata inviata fuori dal Sistema Solare per non farvi più ritorno.
Domande poste dagli utenti: