|
Pitagora di Samo era un filosofo Greco vissuto intorno al 530 AC, soprattutto nella colonia greca di Crotone nell'Italia meridionale. Secondo la tradizione fu il primo a dimostrare l'asserzione (teorema) che oggi porta il suo nome:
Un angolo retto può essere qui definito come l'angolo formato da due linee rette che si intersecano in modo che tutti e 4 gli angoli ottenuti siano uguali. Il teorema funziona anche all'inverso: se la lunghezza dei tre lati (a,b,c) di un triangolo soddisfa la relazione di cui sopra, allora l'angolo tra i lati a e b deve essere di 90 gradi. Per esempio, un triangolo di lati a = 3, b = 4, c = 5 (pollici, piedi, metri--ciò che si vuole) è un rettangolo, perché a2 + b2 = 32 + 42 = 9 + 16 = 25 = c2 Gli antici costruttori Egiziani possono aver conosciuto il triangolo (3,4,5) ed averlo usato (con aste o corde graduate) per costruire angoli retti; anche i costruttori di oggi possono ancora inchiodare assieme delle tavole di quelle lunghezze per rettificare un angolo. Esistono diverse dimostrazioni e quelle più semplici sono probabilmente quelle basate sull'algebra, usando le identità elementari discusse nella sezione precedente, cioè 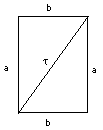
(a + b)2 = a2 + 2ab + b2 (ricordiamo che 2ab significa 2 volte a per b). Per esempio:
= 102 + (2)(10)(5) + 52 = 100 + 100 + 25 = 225 e (a – b) 2 = a2 – 2ab + b2 Per esempio:
= 102 – (2)(10)(5) + 52 = 100 – 100 + 25 = 25 È anche necessario conoscere alcune semplici aree: l'area di un rettangolo è (lunghezza) per (ampiezza), così l'area di quello disegnato sopra è ab. Un taglio diagonale lo divide in due triangoli rettangoli con i lati corti a e b, e l'area di tale triangolo è perciò (1/2) ab. 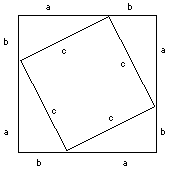
Ora guardate il quadrato sulla sinistra costruito su quattro triangoli (a,b,c). La lunghezza di ogni lato è (a+b) e perciò l'intero quadrato ha un'area di (a+b)2. Tuttavia, il quadrato può anche essere diviso in
quattro triangoli (a,b,c) più un quadrato
di lato c al centro (a rigor di termini,
dovremmo anche provare che è un quadrato,
ma salteremo quella parte). L'area di ogni triangolo,
come mostrato prima, è (1/2)ab, e
l'area del quadrato è c2. Dal
momento che il quadrato grande è uguale alla
somma di tutte le sue parti (a + b) 2 = (4)(1/2)(a)(b) + c2 Usando l'identità per (a + b)2 e moltiplicando (4)(1/2) = 2 a2 + 2ab + b2 = 2ab + c2 Sottraete 2ab da ambo i membri e vi rimane a2 + b2 = c2 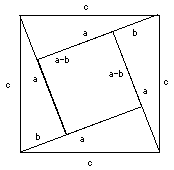
Lo stesso risultato può anche essere visualizzato utilizzando un quadrato diverso, di area c2. Come mostra il disegno sulla destra, tale area può essere divisa in 4 triangoli come quelli di prima, con in più un piccolo quadrato di lato (a– b). Abbiamo c2 = (4)(1/2)(a)(b) + (a– b) 2 = 2ab + (a2 – 2ab + b2) = a2 + b2 Q.E.D. Q.E.D. sta per "quod erat demonstrandum", in Latino per "come volevasi dimostrare", e nei libri di geometria tradizionali quelle lettere denotano la fine di una dimostrazione. L'importanza del lavoro di Pitagora e dei successivi maestri della geometria greca (specialmente Euclide) fu non solo in cosa essi dimostrarono, ma del metodo che svilupparono: partire da alcune affermazioni elementari che sono assunte come valide ("assiomi") e dedurre con la logica le loro conseguenze più complicate ("teoremi"). La Matematica segue ancora lo stesso modello. Per una applicazione pratica del teorema di Pitagora--ricavare la distanza dall'orizzonte (trascurando gli effetti atmosferici)--si guardi qui. |