|
I triangoli si presentano in molte forme. Sarebbe difficile classificare triangoli di forma arbitraria, ma osserviamo che ogni triangolo ABC può essere sempre diviso in due triangoli rettangoli, triangoli con un angolo uguale a 90°. Quelli sono più facili da trattare. 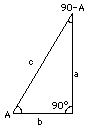
La somma dei tre angoli di un triangolo è di 180o (qui non lo dimostreremo) e perciò, in un triangolo rettangolo con angoli acuti A e B A + B + 90° = 180° Sottraendo 90° da ambo i membri A + B = 90° Dato il valore di un solo angolo A, l'altro angolo B è completamente determinato (è uguale a 90°−A), e così pure è la forma del triangolo, sebbene non la sua dimensione. Siano (a,b,c) i lati del triangolo, ciascuno corrispondente al nome dell'angolo opposto ad esso. L'angolo A non determina la lunghezza di alcun lato, ma stabilisce unicamente i rapporti tra i lati. Questi rapporti hanno dei nomi, ed esiste una specifica notazione per scriverli: a/c = sen A -- "il seno di A" Per distinguerli, basta ricordare: sen A ha il lato opposto all'angolo A al numeratore della sua frazione Esiste una semplice relazione tra il seno e il coseno di ciascun angolo. Perché per il teorema di Pitagora a2 + b2 = c2 Perciò, per ogni angolo A (sen A)2 + (cos A)2 = (a2/c2) + (b2/c2) = (a2 + b2)/c2 = 1 Questa relazione è espressa di solito con il quadrato scritto sen2A (e non senA2, che potrebbe essere intesa come il seno di un angolo uguale ad A2): sen2A + cos2A = 1 Entrambi senA e cosA devono essere numeri più piccoli di 1, perché i lati di un triangolo adiacenti e opposti sono sempre più corti del lato opposto all'angolo di 90° (chiamato ipotenusa, una parola cara agli amanti di scherzi e giochi di parole (in inglese si dice hypotenuse, la cui pronuncia è la stessa di "hi pot and noose" ovvero "ciao pentola e cappio")). Quando l'angolo A diventa prossimo a 90° (e B diventa sempre più piccolo), il triangolo diventa sempre più stretto e lungo. La lunghezza del lato a quindi si avvicina a quella di c, mentre la lunghezza di b diventa molto piccola: perciò quando A si avvicina a 90°, senA si avvicina a 1 e cosA si avvicina a zero. Per il calcolo di ulteriori valori, si veda il prossimo paragrafo. |