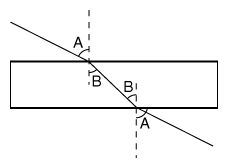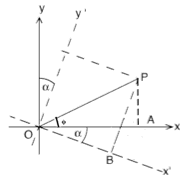
- In un sistema di coordinate cartesiane il punto P ha coordinate (x,y), e come mostrato nel disegno, x = OA, y = PA.
Un secondo sistema con la stessa origine O ha gli assi (x',y') ottenuti ruotando gli assi (x,y) in senso orario di un angolo α. Nello stesso disegno, le nuove coordinate di P sono x' = OB y' = PB.
Utilizzando i punti ausiliari (C,D,E) e le linee ausiliarie AE e AD, esprimiamo x' e y' in funzione di x, y, senα e cosα.
Suggerimento (seguite questo passo dopo passo nel disegno). I due triangoli CBO e CPA sono rettangoli, e siccome la somma degli angoli in un triangolo rettangolo è 180°, la somma dei due angoli acuti in ciascuno di essi è 90°. Di quegli angoli acuti, i due che si incontrano in C sono uguali, e perciò gli altri due devono anch'essi essere uguali.
Di quegli altri angoli AOB è uguale ad α. Perciò l'angolo APC è anch'esso uguale ad α, come indicato. Cercate di risolvere il problema prima di continuare.
Soluzione
Ricordate: in un triangolo rettangolo con un angolo α, se si moltiplica il lato lungo (o ipotenusa)
- per cosα, si ottiene il lato adiacente ad α
- per senα, si ottiene il lato opposto ad α
Questo suggerisce di prestare una speciale attenzione ai triangoli rettangoli i cui lati lunghi sono x e y, cioè i triangoli OAD e PAE. Se possibile, cercheremo di esprimere x' e y' in funzione dei lati di quei triangoli.
x' = OB = OD–BD = OD–AE = OA cosα – AP senα = x cosα – y senα
y' =BP = BE+EP = AD+EP = OA senα + AP cosα = x senα + y cosa
Riscriviamo il risultato finale:
x' = x cosα – y sinα
y' = x sinα + y cosα
Esercizio di Algebra: utilizzando le due relazioni di cui sopra, sapete esprimere (x,y) in funzione di (x',y')?
Dovete usare sen2α + cos2α = 1.
Mostrate anche che il risultato è consistente con la prima formula, se scambiamo i ruoli di (x,y) e (x'y') e sostituite l'angolo di rotazione con (– α).
Ciò sarebbe anche in accordo con la figura, in quanto (x,y) sono ottenute ruotando (x',y') in senso antiorario di un angolo α, che può essere visto come una rotazione in senso orario di un angolo (– α).
Cliccate qui per una ulteriore discussione di questo risultato, specialmente per quelli che hanno studiato la sezione #12A "Come Vengono Calcolate le Orbite."
- Quanto è lunga la linea della latitudine L se la Terra è una sfera e la distanza equatore-polo è 10.000 km? Quanto è lungo un grado di longitudine alla latitudine L?
La formula vale anche per la latitudine meridionale?
- (a) Se cos X = 2 senX, quanto vale sen X? Quanto vale l'angolo X?
(b) Questa è l'unica soluzione?
Suggerimenti:
(a) Usate cos2X = 4 sen2X
(b) Siccome lavoriamo con un'equazione che contiene solo quadrati, ogni sua soluzione porta solo a sen2X e cos2X. Tuttavia, la condizione originale richiede anche che cos X and sen X abbiano lo stesso segno algebrico.
|
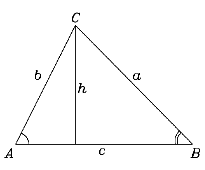
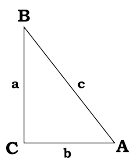 Un triangolo ABC ha un angolo retto C e due angoli acuti A e B. I lati AC e BC del triangolo, da ambo le parti dell'angolo retto, sono dati di seguito:
Un triangolo ABC ha un angolo retto C e due angoli acuti A e B. I lati AC e BC del triangolo, da ambo le parti dell'angolo retto, sono dati di seguito: