#21c     Vuelo a Marte: Cálculos

    En la sección anterior la ruta a Marte fue identificada: era una elipse de transferencia Hohmann. El tiempo requerido también se dedujo, aproximadamente 8,5 meses, así como la posición de Marte en el momento del lanzamiento, alrededor de 45º después de la aproximación más cercana.

    En esta sección calculamos dos detalles esenciales: el aumento de velocidad necesario para inyectar la nave espacial a Marte dentro de la órbita de transferencia, y la velocidad de llegada a la órbita de Marte. ¿Pasará la nave al planeta o será pasada por éste?, y ¿cuál será el desfase de velocidad entre la nave y el planeta, un desfase que probablemente requerirá un impulso adicional del cohete?. Siga leyendo y, si domina el álgebra elemental, podrá averiguarlo.

Notación y velocidades de escape

    Antes de comenzar, será de ayuda establecer una notación para las cantidades usadas aquí. Aún cuando algunas de ellas son vectores, solamente utilizaremos sus magnitudes. Se usa negrita solamente para remarcar, nunca para indicar que se trate de un vector.

    Como antes, r₁ = 1 AU es la distancia de la Tierra desde el Sol, r₂ = 1,523691 AU la de Marte, y (como aproximación) se asume que ambos planetas se mueven en círculos.

    La velocidad V tendrá unidades de kilómetros por segundo (km/s), y otras velocidades serán identificadas con subíndices. La v minúscula identifica velocidades asociadas con órbitas alrededor de la Tierra en vez de alrededor del Sol.

    La sección anterior también introdujo la velocidad órbital V₀ de la tierra alrededor del Sol, que es de alrededor de 30 km/s (aprox.), mucho mayor que v₀ ~ 8 km/s (aprox.) requerida por un satélite para rodear la Tierra sobre su superficie (ignorando la atmósfera). En la sección #21 hicimos notar que la velocidad de escape v_e desde una órbita tan baja se obtiene multiplicando v₀ por la raíz cuadrada de 2, que vale 1,41421356.... aproximada aquí en 1,414. Esto da:
   

v_e = 1,414 v₀ = (1,414)(8) = 11,312 km/sec

    Tal astronave, sin embargo, aún no es libre de moverse a cualquier punto en el espacio. La velocidad v_e ha obtenido su libertad de la gravedad Terrestre, pero no la libertad de la atracción del Sol, alrededor del cual continúa moviéndose en una órbita similar a la de la Tierra, a V₀ =30 km/s .

    La situación ahora es completamente análoga a escapar de una órbita de baja altitud (¡excepto que el coste es mayor!). Para liberarse de una órbita circular alrededor del sol y abandonar el sistema solar, la nave espacial necesita aumentar su velocidad a una "segunda velocidad de escape":
   

V_e = 1,414 V₀ = (1,414)(30) = 42,42 km/s   (aprox.)

    Para alcanzar V_e la nave debe incrementar de alguna manera su velocidad en 12,42 km/s adicionales, ¡más de lo que se necesita para escapar de la gravedad de la Tierra, partiendo desde la superficie!. Afortunadamente, existen maneras (tratadas en la Sección #35) de hacer que el movimiento de los planetas (o de la Luna) provean parte de este impulso.

    Otras velocidades que entran en el cálculo son la velocidad V₁ con la cual la nave espacial parte desde cerca de la Tierra y entra a la elipse de Hohmann (distancia r₁ desde el Sol), y la velocidad V₂ con la cual ésta alcanza la órbita de Marte (distancia r₂). Además, V₃ será la velocidad de Marte en su órbita, asumiendo que ésta tiene una magnitud constante (es decir, suponiendo que la órbita de Marte es circular). Si V₂ > V₃, la nave espacial sobrepasa a Marte, mientras que con V₂ < V₃ la nave será sobrepasada.

Ecuaciones requeridas

    (1) Leyes de Kepler

•     La primera ley es: "Los Planetas se mueven en elipses, con el Sol en uno de los focos". Esto ya lo estamos usando; por ejemplo, la elipse de transferencia es una de esas órbitas.

•     La segunda ley es: "La línea imaginaria que conecta un planeta con el Sol barre áreas iguales en tiempos iguales". Permítasenos intentar extraer de esto una ecuación útil.

Aplicación de la 2da. Ley de Kepler

    El dibujo aquí muestra la órbita de Marte (línea sólida) y la elipse de transferencia (línea partida), con radios (r₁, r₂) a los puntos (de perigeo y apogeo), en los cuales la velocidad de la nave espacial es (V₁, V₂). Los segmentos cortos dibujados en esas posiciones representan la distancia cubierta por la nave espacial en el siguiente segundo después de pasar el perigeo o el apogeo y, por la definición de velocidad ("distancia por segundo") su valor es igual (en km) al de V₁ y V₂. En realidad, esos segmentos deberían ser curvos como la órbita pero, siendo tan cortos, difieren de forma insignificante de las líneas rectas. Completamos entonces los triángulos largos y delgados, que tienen como base esos segmentos.

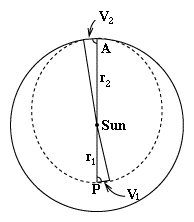
    Note que cada uno de estos triángulos tiene un ángulo recto en la parte inferior, porque en el apogeo y en el perigeo (y en ningún otro lugar), la línea del Sol es perpendicular a la órbita.

    En el perigeo, la altura del triángulo es r₁, la longitud de su base es V₁, entonces por la ecuación para el área A₁ de un triángulo
   

A = (1/2) (altura) (base)

obtenemos

A₁ = (1/2) r₁ V₁

    En el apogeo, la altura es r₂, la base V₂, y el área es
   

A₂ = (1/2) r₂ V₂

    Cada uno de estos triángulos es barrido en un segundo, entonces, por la segunda ley de Kepler sus áreas pueden ser consideradas iguales. Multiplicando por 2 ambos lados de esa equivalencia:
   

r₁ V₁ = r₂ V₂                     (1)

    Numeramos la ecuación para poder referirnos a ella más adelante. Por favor, note que esta relación solamente se cumple entre el apogeo y el perigeo. En los demás puntos de la órbita el ángulo entre el radio y la órbita no es 90º, y el área también depende del valor exacto de ese ángulo.

    La tercera ley de Kepler ya fue usada para determinar el periodo orbital. La necesitaremos nuevamente al final.

    (2) La Ecuación de La Energía

    En la sección #12 establecimos que la energía E de un satélite de masa m órbitando la Tierra, en cualquier punto de su órbita, es

E = (1/2) mV²   –   km / r                     (2)

donde r es la distancia al punto desde el centro de la Tierra, V es la velocidad del satélite en ese punto, y k es alguna constante relacionada con la aceleración gravitacional g. Debido a que la energía E se conserva, la expresión de la derecha tiene el mismo valor en cualquier lugar de la órbita. Una relación similar se mantiene para órbitas alrededor del Sol, aunque el valor de k es diferente. Podemos expresar k en ese caso usando un simple truco, basado en la velocidad de escape.

    Como notamos anteriormente, para que un objeto en la órbita terrestre escape completamente (¡pero justito!) de la órbita del Sol, necesita una velocidad V_e = 1,414V₀ = 42,42 km/s (aprox.). Sea E₀ la energía de tal objeto. Entonces si

V_e² = 2 V₀²

obtenemos (en la órbita terrestre)

E₀ = m V₀²   −   km / r₁

    Debido a que éste tiene velocidad de escape, si esperamos un largo, largo tiempo, este objeto estará extremadamente lejos de la Tierra y, habiendo agotado prácticamente toda su energía cinética, su velocidad será muy cercana a cero. Entonces ambos términos del lado derecho de la ecuación (2) tienden a cero, sugiriendo
   

E₀ = 0

            se ajusta al significado del signo de E:

E negativa siempre identifica órbitas “elípticas” ligadas al Sol, como la de los planetas. E positiva caracteriza trayectorias “hiperbólicas” no ligadas, como la de la sonda espacial Voyager 2, mientra abandona el sistema solar y entra en la profunda oscuridad que hay más allá, siempre manteniendo una velocidad importante. Y los movimientos con E=0 son “parabólicos” y caen en el límite entre los otros dos grupos (de órbitas), no limitados en distancia pero desacelerándose a medida que la distancia crece. Las órbitas de los cometas no periódicos están cercanas a este comportamiento.

Así que tenemos:

m V₀²   −   km / r₁ = 0

    Dividiendo por m y cambiando el término negativo V_e a la derecha

V₀² = k / r₁

    por lo cual el valor de k podría ser escrito
   

                            k = V₀² r₁                     (3)              

Cálculos

    Volviendo ahora a la nave espacial en la órbita de transferencia hacia Marte, su energía debería ser la misma en el perigeo P y en el apogeo A, entonces por la ecuación (2)

1/2 m V₁²   –   km / r₁   =   1/2 mV₂²  −   km / r₂

    Dividimos ambos lados por m ("cancelamos m") y multiplicamos ambos lados por 2:

V₁²   −   2 k / r₁   =   V₂²   −   2 k / r₂

Transfiriendo términos (mediante la adición de las cantidades convenientes en ambos lados) y sustituyendo (3) da

V₁²   −   V₂²   =   2 V₀² r₁ (1/ r₁   −   1/r₂)  

                                        =   2 V₀² (1   −   (r₁/r₂))                     (4)

                    V₂ = V₁ (r₁/r₂)                     (5)

Elevando al cuadrado

V₂² = V₁²(r₁²/r₂ ²)

    Sustituyendo esto en el lado izquierdo de (4)

V₁² – V₂²   =   V₁² (1   –   (r₁²/r₂²))

mostrando que necesitamos adicionar sólo 2,945 km/s, una pizca menos de 3 km/s, ó un 10% de la velocidad orbital.

Llegada a Marte

La velocidad V₂ a la cual la nave llega a Marte se encuentra en (5)
   

    Ha consignado una parte de su energía cinética para contrarrestar la atracción del Sol y moverse alejándose del Sol. La gran pregunta ahora es: ¿cómo queda esta velocidad al compararla con la velocidad V₃ de Marte en su órbita?

    Para obtener velocidades en km/s, las distancias deben estar medidas en kilómetros, y los tiempos en segundos, pero por el bien del “ciudadano de a pie”, dividiremos los cálculos, evitando números grandes y la notación científica. Comenzamos con la 3er. ley de Kepler para órbitas circulares, con distancia r en AU y periodo órbital T en años. Como surge de la sección precedente, (y también en la sección #10), en estas unidades

T² = r³

    Para Marte, r = 1,523691, T² = (1,523691)³ = 3,53745

T = 1,8808 años

T = 1,8808 años = 686,96 días

    Durante ese tiempo la nave espacial cubre

2 π r = (6,2832) (1,523691) (149,598,000) km =

= (1432,2) (1.000.000) km

    Dividiendo por T, se llega a

(1432,2 / 686,96) (1.000.000) = (2,08484) (1.000.000)

                       = 2.084.840 km/día

Cada día tiene (24)(3600) = 86400 segundos, entonces la distancia órbital cubierta por Marte cada segundo es

2.084.840 / 86.400 = 24,130 km

    Distancia por segundo es, por supuesto, la definición de velocidad. Por lo tanto

V3 = 24,130 km/s

Comparando con

V2 = 21,481 km/s

Vemos que Marte es el que se mueve más rápido, y sobrepasará a la nave espacial. Para igualar velocidades con Marte, la nave debe general un impulso extra de 2,649 km/s.