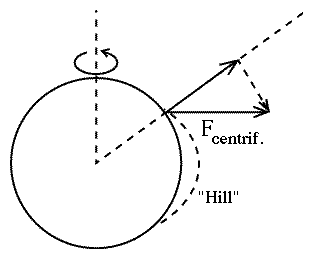
By now you should realize what this gives us--an explanation to the equatorial bulge of the Earth! That bulge is nothing but the "hill" described above, and the shape of the surface is such that the ground is always perpendicular to the effective gravity
Jupiter rotates in just under 10 hours and has an equatorial radius about 11 times that of Earth, creating a much stronger centrifugal force. As a result, in spite of a surface gravity 2.64 times stronger than Earth's, Jupiter is much more oblate, by about 6.5%.
 The oblateness of Jupiter was noted through the telescope by Giovanni Cassini (1625-1712), director of the Paris observatory, However, he and his son also claimed that Earth was different, that it bulged at the poles (more like a lemon than like a grapefruit). They based their claim on measurements on the ground, which suggested lines of latitude became closer together as one approached the pole.
The oblateness of Jupiter was noted through the telescope by Giovanni Cassini (1625-1712), director of the Paris observatory, However, he and his son also claimed that Earth was different, that it bulged at the poles (more like a lemon than like a grapefruit). They based their claim on measurements on the ground, which suggested lines of latitude became closer together as one approached the pole.
Their result was later disproved by more accurate observations, but even before that, Newton by the following simple argument showed this could not be so. Assume Earth is a sphere, and imagine two deep holes extending to its center (see drawing), meeting there and filled with water. If Earth did not rotate, one may have expected the height of each water column to be the same: at the center of the Earth, by symmetry, each column would push down with the same weight, creating an equilibrium.
On a rotating Earth, however, the centrifugal force acts to reduce the weight of the water in the equatorial hole, and the water would rise there to greater height. Newton then argued that water anywhere would rise to the same level
|
|
...if our earth were not a little higher around the equator
than at the poles, the seas would subside at the poles and, by ascending in the region of the equator, would flood
everything there.
|
Jet planes above the equator
(Thanks to John Lowry for this neat example!)
The centrifugal force is a useful concept when figuring out equilibria in a rotating frame of reference, cases where forces balance exactly and no motion occurs.
To calculate motion in a rotating frame is much more complicated, and in general is beyond the level of this presentation. All that will be done in this section and the one that follows is point out some complications.
Let us assume the reduction of effective gravity is the same at jet-plane altitude--a small difference exists, but does not affect the argument below. Two jet airplanes fly along the equator at equal speeds--one eastwards, the other westwards. Since they fly in circles around the center of Earth, the effective gravity aboard each of them is further changed. Do both sense the same change?
You might think so, but it isn't true.
It would be the same if the Earth did not rotate (neglect here the attraction of the Sun and the rotation of the Earth around it, two effects which about balance). Without Earth rotation, in the frame of the universe, the eastward and westward motions are completely symmetric.
Actually, however, the speeds of the jets are measured relative to that atmosphere, which itself also rotates around the center of the Earth. Viewed from the frame of the universe, the speed of the Eastward jet is added to the rotation of the atmosphere, the one of the westward jet is subtracted.
Suppose these are two supersonic Concorde airliners, flying at 465 meter/sec (or whatever is the speed of the atmosphere around them as it co-rotates with the surface below). Rather than study the motion in a rotating frame, which may or may not give correct answers, we can always go back to the non-rotating frame of the universe. In that frame, the rotational velocity of the westward jet is zero, and it senses no effective reduction of gravity. In the same frame, the eastward jet has twice the velocity, and since the centrifugal force is proportional to the velocity squared (v2), it senses four times the centrifugal force. Effective gravity aboard that jet is reduced by four times the amount felt on the ground, or 1.384%.
For airplanes flying east and west above the equator. this is essentially a modification of the centrifugal force. If the planes flew east and west at (say) latitude 35, the calculation would be more complicated (for the formula, see StarFAQ26.htm#492)
What it means
The above example suggests that we better watch out before applying Newton's laws in a rotating frame.
Newton's first law certainly does not hold--a body not acted on by any force will not stay at rest but will fly off at a tangent. One can salvage this part of the law by adding a centrifugal force in any calculation of balanced forces. But if such forces are not balanced, if they cause motion in the rotating frame, then a modified form of Newton's laws must be used. They do exist, but are beyond the level of this course. The above example suggests some of the problems of rotating frames, and more examples are in the next section, which tells about the Coriolis effect.
You and I, and anyone else on Earth, live in a rotating frame of reference. Should we therefore refrain from using Newton's equations in everyday life? It turns out that for motions on a scale much smaller than the size of Earth, at moderate velocities, the effects are negligible.
One example concerns the famous question of whether draining water in kitchen sinks on opposite sides of the equator swirls in opposite directions, as is sometimes claimed. It turns out (see next section) that the effect in principle exists, but is much too small to affect observations. In the world wars, gunners firing big cannons corrected their aim (slightly) to account for the Earth's rotation, but you and I can usually ignore it, except for the modification of gravity by the centrifugal force.
Questions from Users:
 The oblateness of Jupiter was noted through the telescope by Giovanni Cassini (1625-1712), director of the Paris observatory, However, he and his son also claimed that Earth was different, that it bulged at the poles (more like a lemon than like a grapefruit). They based their claim on measurements on the ground, which suggested lines of latitude became closer together as one approached the pole.
The oblateness of Jupiter was noted through the telescope by Giovanni Cassini (1625-1712), director of the Paris observatory, However, he and his son also claimed that Earth was different, that it bulged at the poles (more like a lemon than like a grapefruit). They based their claim on measurements on the ground, which suggested lines of latitude became closer together as one approached the pole.