(E-5) Reti di Resistori: Uso della Legge di Ohm
Molti carichi agiscono da resistori (nella pratica il resistore viene chiamato con la sua grandezza fisica "resistenza") – i fili incandescenti nei tostapane o nei forni, o i filamenti luminosi nelle lampadine "a incandescenza". Altri carichi possono spesso essere approssimativamente trattati come resistori – ad esempio i ventilatori in un circuito a corrente alternata, anche se essi possono influenzare la forma d'onda della tensione. Qui verranno studiati solo i circuiti più semplici, quelli che impiegano resistori e correnti stabili (continue o alternate). Le correnti in ciascuno di essi possono essere ricavate dalla legge di Ohm
Questo vale per qualsiasi porzione del circuito: se V è la caduta di tensione ai suoi capi ed R la sua resistenza, allora I è la corrente che circola in esso. Naturalmente, in corrispondenza di un nodo del circuito a cui afferiscono diversi conduttori, la somma delle correnti entranti nel nodo deve essere sempre uguale alla somma di quelle uscenti da esso.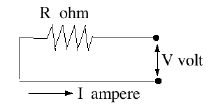 
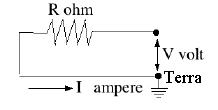
Per convenzione comune, un resistore (senza altre proprietà elettriche) viene indicato da una linea a zig-zag, con il valore della resistenza indicata dalla Ω , la lettera maiuscola greca omega. (i kilo-ohm o migliaia di ohm sono indicati da kΩ ; i mega-ohm o milioni di ohm da MΩ ; maggiore è la resistenza, minore è la corrente che può attraversarla!)
Nel diagramma sopra, supponiamo che la resistenza sia R=12Ω e che quando l'interruttore è chiuso, la tensione all'estremità destra del resistore sia V=9 volt. L'altro lato del resistore è collegato a terra e la corrente è pertanto
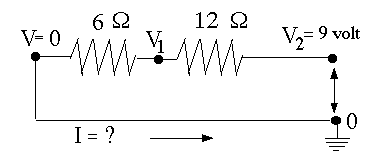
Supponiamo che il circuito contenga due resistori collegati tra loro alle estremità o "in serie", così che la stessa corrente I passi per entrambi (i resistori "in serie" sono già stati incontrati in precedenza, in modo più casuale). Come prima si colleghi l'estremità destra a V2, l'estremità sinistra a terra e la tensione nel punto intermedio si indichi con V1. Se i resistori sono di 12Ω e di 6Ω, la legge di Ohm deve essere soddisfatta in ogni segmento, così
Un'equazione supplementare, ma anche una variabile sconosciuta aggiuntiva, V1 (ci viene dato V2 = 9 volt). Utilizzando il fatto che la corrente I che affluisce nel nodo al centro è uguale alla corrente I che defluisce da esso, questa può essere ridotta ad una equazione
dividendo per 3 e scambiando i membri: V1 = 3 volt La corrente può essere calcolata da una delle due equazioni (entrambe devono dare lo stesso risultato), ad esempio La corrente è più piccola di prima, perché è stata inserita una ulteriore resistenza. Si noti che due resistori di 12Ω e 6Ω in serie agiscono come un singolo resistore di (12+6)=18Ω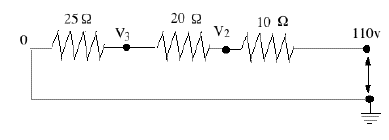 
Un altro esempio, con una sorgente di alimentazione in corrente alternata e 3 resistori in serie, viene mostrato sopra. In un circuito a corrente alternata, la tensione cambia costantemente e inverte la polarità, e il valore di 110 volt è in realtà una sorta di media (implicando che 110V in corrente continua fornirebbe altrettanta energia). Ma poiché semplici resistori gestiscono corrente continua e alternata nello stesso modo, possiamo altrettanto bene far finta di avere 110V in corrente continua. Se I è la corrente, V1 = 110 volt, e (V2, V3) le tensioni intermedie (l'estremità destra si trova a zero come prima), allora (1) I = (110 – V2)/10 o 10 I = 110 – V2(2) I = (V2 – V3)/20 o 20 I = V2 – V3 (3) I = (V3)/25 o 25 I = V3 Si sommino insieme La stessa procedura può essere applicata a qualsiasi numero di resistori in serie: l'effetto combinato è lo stesso di una singola resistenza R pari alla somma, per esempio Un Partitore di TensioneUn partitore di tensione è tipicamente un filo sottile con resistenza apprezzabile avvolto attorno ad un lungo tubo (rettilineo o curvo), con un contatto mobile nel mezzo. Si veda lo schema: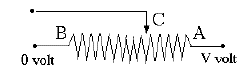
Le manopole rotanti su una radio o su un altro strumento sono verosimilmente collegate a partitori di tensione. Il contatto strisciante C (punta di freccia) può toccare qualunque tensione tra V (quando tocca A) e zero (quando tocca B), e di conseguenza regolare il volume del suono, la luminosità del display o qualche altra uscita. 
Spesso il contatto strisciante va all'ingresso di un amplificatore, in modo da assorbire solo una piccola corrente e non creare una variazione apprezzabile del fabbisogno di energia. Solo se A e C sono collegati, questo diventa un resistore variabile, ma allora la potenza assorbita varia ampiamente con la regolazione. Negli schemi circuitali i resistori variabili sono contrassegnati da una linea a zig-zag per il resistore, attraversato diagonalmente da una freccia. I resistori sono elementi importanti in molti dispositivi. In una radio, le correnti sono piccole e non generano molto calore, così i resistori sono spesso piccoli cilindri di plastica dalle cui estremità sporgono i fili di connessione. L'elemento di resistenza è molto simile alla mina di una matita, che conduce l'elettricità contenendo la grafite, una forma di carbonio. Qui il carbonio può essere finemente mescolato con una sostanza non conduttiva, per controllare la resistività, oppure uno strato conduttivo viene deposto sul nucleo.
I resistori "ad avvolgimento" hanno uno speciale filo metallico avvolto attorno ad un tubo ceramico, ricoperto di smalto isolante. Essi tendono ad essere più stabili e possono sopportare temperature più alte, vale a dire correnti più grandi.
|
Si noti che conta solo la differenza di tensione. Nelle formule sopra, V significa proprio "la differenza di tensione tra le estremità del resistore". In altre parole, il valore assegnato alla tensione (o "potenziale elettrico") in qualsiasi punto è generalmente definito solo rispetto ad altri punti. L'ambiguità può essere rimossa scegliendo – ai fini del calcolo – un punto che abbia tensione zero. Nei circuiti reali, questo è solitamente un punto collegato a terra che, sebbene non sia sempre un buon conduttore come il metallo, è abbastanza grande per mantenere una tensione costante che può servire come riferimento. Negli schemi il terreno è indicato da una serie di brevi linee orizzontali, la cui lunghezza diminuisce verso il fondo così da occupare lo spazio di un triangolo.