(E-6) Ancora Reti di ResistoriLa stessa corrente I li attraversa tutti, ma la tensione V applicata è suddivisa tra i resistori in proporzione alla loro resistenza – la maggior parte della tensione ricade sulla resistenza più grande, la minor parte su quella più piccola.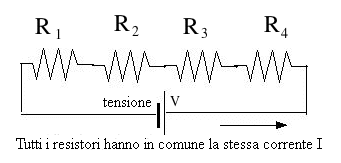 
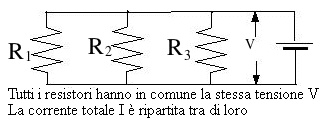
L'altro schema di collegamento "standard" di resistori è quello in parallelo – tutti i resistori ricevono corrente dallo stesso punto e la cedono ad uno stesso punto.
Collegando le celle in parallelo si ottiene la stessa tensione di una singola cella, ma si può prelevare una corrente molto maggiore senza dar luogo a sovraccarico. Tuttavia, sarebbe meglio che tutte le celle fornissero la stessa tensione, altrimenti quelle in grado di fornire una tensione più elevata inizierebbero a caricare quelle con tensione più bassa.)
Un insieme di resistori in parallelo
R1, R2, R3,...
può anche essere sostituito da "una resistenza equivalente" R. Supponiamo di avere 3 resistori. Siccome tutti sono alimentati dalla stessa tensione V e la legge di Ohm è soddisfatta da ciascuno di essi, le loro correnti sono
Quindi la corrente totale è Quindi, se R è la resistenza equivalente del circuito Se, come nella sezione precedente La regola è: le resistenze in serie hanno una resistenza equivalente più grande di ciascuna di esse, mentre le resistenze in parallelo hanno una resistenza equivalente più piccola di ciascuna di esse. Problemi pratici da risolvere:
(2) Resistori da 60Ω, 90Ω e 150Ω in parallelo... R = ? Applicazioni
Gli impianti elettrici domestici vengono sempre cablati a tutte le prese e interconnessioni in parallelo, perché ciascuna di esse deve essere alimentata alla stessa tensione di 110v (220v in Europa). Si supponga di aver realizzato in una stanza un impianto elettrico per alimentare due lampadine identiche, e che una volta attivato il circuito, entrambe le lampadine si siano accese insieme (come previsto) – ma i loro filamenti erano fiochi e risplendevano debolmente. Perché? Molto probabilmente perché per errore entrambe le lampade sono state cablate in serie, non in parallelo, così che la stessa corrente circola in entrambe e ciascuna riceve solo 55 volt. Vogliamo assicurarcene? Svitiamone una – si spegnerà anche l'altra. Naturalmente, la corrente totale che si può prelevare da un impianto elettrico domestico è limitata. Se si collegano troppe luci ed eletrodomestici, o in qualche modo si mettono in contatto diretto fili elettrici a tensioni opposte (un "corto circuito" con una resistenza molto piccola), il circuito in questione preleverà una corrente elettrica molto grande. Come discusso più avanti nella sezione 8, ciò rilascia troppi "watt" di energia elettrica nei fili in cui circola la corrente, surriscaldandoli pericolosamente. Nella maggior parte delle case, un fusibile o un interruttore (discusso più avanti) interromperà allora l'alimentazione, e il circuito si spegnerà. Quello sarà l'avvertimento – prima che una eccessiva corrente sciolga i fili dell'impianto, bruci l'isolamento o magari dia luogo ad un incendio in casa; le cronache dei giornali sugli incendi spesso finiscono con "...il capo dei pompieri ritiene che l'incendio abbia avuto origine elettrica", ed è così che succede.
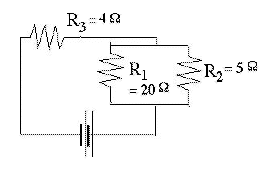
Per calcolare la corrente assorbita da un circuito più complicato, si può spesso iniziare col sostituire combinazioni di resistori con delle resistenze equivalenti. Per esempio, col circuito mostrato qui
si sostituiscono dapprima i due resistori in parallelo con la loro resistenza singola equivalente R4
Quindi R4 = 4Ω e la resistenza equivalente dell'intero circuito è Una tale situazione si verifica con batterie e celle sottoposte a un carico elevato. La corrente che forniscono deve vincere non solo la resistenza del circuito esterno, ma anche la resistenza interna Ri del liquido conduttore ("elettrolita") che chiude il circuito all'interno della batteria o della cella (di sicuro questo è uno schema semplificato). Ri generalmente è piccola, ma pone un limite alla corrente che può essere prelevata, anche quando le estremità sono collegate direttamente ("cortocircuitate").
Il circuito di cui sopra (concettualmente, non nei valori reali) può essere visto come la rappresentazione del circuito di un'auto, con R3=4Ω la resistenza interna della batteria (il valore reale probabilmente è molto minore), e R1=20Ω la resistenza dei fanali, che assorbe una corrente moderata. Una certa tensione può cadere sulla resistenza R3, ma non molta. Tuttavia, quando il motorino di avviamento viene collegato (rappresentato da R2=5Ω) il carico effettivo con Ri=4Ω eguaglia la resistenza interna della batteria, e perció solo la metà della tensione disponibile appare attraverso il circuito AB dei fanali.
Analisi dei nodi (facoltativo)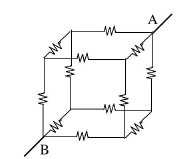
Non tutti i circuiti di resistori possono essere ricondotti a combinazioni di resistori in parallelo e in serie. Consideriamo un problema "classico" che compare in molti libri di testo: Una tensione di 10V viene applicata tra i vertici opposti (A,B) di un cubo che consiste di 12 resistori di 1Ω ciascuno. Quanta corrente circolerà – o in altre parole, quanto vale la resistenza equivalente R tra A e B?
Questo circuito non può essere ricondotto a gruppi di resistori in parallelo e in serie (almeno non nel solito modo).
Tale metodo si basa sull'idea che in ogni rete di resistori complicata collegata ad una certa tensione di alimentazione, ogni n-esimo resistore Rn, la sua corrente In e la differenza di tensione ΔVn tra le sue estremità (delta o Δ [D maiuscola in greco] generalmente indica una "differenza") sono collegate dalla legge di Ohm Finché quella legge è valida, la resistenza di un insieme di resistori rimane la stessa per qualsiasi tensione applicata, quindi supponiamo che ΔV = 10V tra A e B – diciamo V=10 in A e V=0 in B, dal momento che la scelta del punto in cui V=0 è arbitraria. Ciò lascia i 6 vertici dei "nodi" nei quali i fili si incontrano, a tensioni V1, V2, V3, ... V6. Le prime 3 tensioni saranno assegnate ai punti (A1,A2,A3) collegati direttamente ad A, le ultime 3 saranno le tensioni di (B1,B2,B3) collegate direttamente a B Esistono anche 6 equazioni, una per ogni nodo, che esprimono la condizione "il flusso entrante uguaglia quello uscente". Sei equazioni con 6 incognite possono generalmente essere risolte: se ne usa una per esprimere V6 in funzione delle altre, si usa la relazione trovata per sostituire V6 nelle restanti 5 equazioni. Quindi si fa lo stesso con V5 riducendo il numero di equazioni a 4, e così via, finché rimane una sola tensione, espressa dalla restante ultima equazione.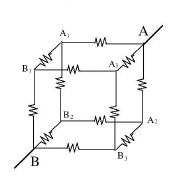 
Se tutti i resistori non fossero uguali, questo tipo di fatica potrebbe essere l'unica strada praticabile (sebbene un programma per computer potrebbe aiutare). Qui tuttavia ogni resistore è uguale agli altri, diciamo di 1Ω, e si può approfittare delle simmetrie. 
Un oggetto ha una forma simmetrica quando lo si può ruotare ed ottenere ancora esattamente la stessa forma. Un cubo ha molte differenti simmetrie: per esempio, lo si metta sul tavolo, lo si ruoti di 90° sul suo lato destro (o sul suo lato sinistro) e si otterrà la stessa forma. Lo si può fare 4 volte, dopodiché si avrà di fronte nuovamente gli stessi lati di prima. Questa è una simmetria rotazionale di ordine 4.
Ma si può anche trovare una simmetria di ordine 3. Si guardi in direzione diagonale verso un vertice del cubo, come nell'immagine sulla destra. Si immagini una sottile asta dritta che entri nel cubo in quel punto e fuoriesca di nuovo dal vertice più distante (l'asta passerà per il centro del cubo). Tre spigoli del cubo fanno capo a quel vertice: se si ruota il cubo intorno all'asta di 120°, esso apparirà di nuovo come quello in figura, ma ora i 3 spigoli hanno cambiato le loro posizioni. Se si ruota 3 volte per 120°, tutti gli spigoli (ed altre parti del cubo) sono tornate dove si trovavano prima: una simmetria rotazionale di ordine 3. Nel cubo di 12 resistori (disegno più grande), il vertice "A" sia il vertice dove è entrata l'asta, il vertice "B" quello da cui essa fuoriesce di nuovo. L'asta è sostituita dai conduttori che trasportano la corrente in A e la prelevano da B; non c'è bisogno della sua porzione centrale e non viene disegnata. Nel punto "A" tre resistori si irradiano simmetricamente verso i punti (A1,A2,A3). A causa della simmetria di ordine 3, le posizioni nel circuito dei 3 resistori che portano ad essi sono completamente equivalenti: non solo essi sono uguali, ma la corrente proveniente da ciascuno continua verso due resistori di 1 Ω, ciascuno dei quali conduce ad uno dei vertici (B1,B2,B3). Questi vertici sono anch'essi completamente equivalenti, per un ragionamento simile. Si conclude che le 3 diverse direzioni in cui si dirigono le correnti elettriche provenienti da A sono completamente simili. Ci si può perció aspettare che le 3 correnti siano uguali. Se la corrente in ingresso ad "A" è uguale ad I ampere, allora ciascuna di tali correnti ha intensità I/3. Per la legge di Ohm, anche la caduta di tensione lungo ciascun resistore collegato ad A è la stessa, così anche la tensione nei punti (A1,A2,A3) deve essere la stessa. La chiameremo V1 Il nodo B ha esattamente la stessa simmetria rispetto a (B1,B2,B3), così se una corrente di I ampere lascia il cubo dal punto B (deve essere uguale alla corrente che entra!), ogni resistore collegato direttamente ad esso trasporta anch'esso una corrente di I/3. Ancora, le tensioni in questi 3 punti dovrebbero essere le stesse, e le chiameremo V2. Infine tutti e 6 i resistori che partono dai punti (A1,A2,A3) hanno lo stesso valore di resistenza (1Ω) e trasportano correnti dalla tensione V1 alla tensione V2. Per la legge di Ohm, ciascuna deve trasportare la stessa corrente, metà della corrente che entra in ciascuno di questi vertici, che vale I/6.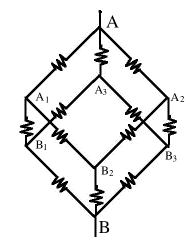 
È tempo ora di raccogliere tutte le informazioni e vedere se da esse possiamo ricavare la relazione tra I e V. Da A fuoriescono tre correnti, ciascuna che trasporta 1/3 della corrente totale I e che soddisfa la
(da qui in poi ometteremo il simbolo Ω). La corrente proveniente da A1 si divide in modo simmetrico in due parti uguali, ciascuna pari a e lo stesso vale per A2 e A3. Infine tre correnti uguali si uniscono di nuovo in B, ciascuna un terzo della corrente totale: Si può anche omettere la divisione per 1. Sommando tutte e tre le equazioni si ha Se R è la resistenza equivalente del cubo, la legge di Ohm dà Se tutti i resistori fossero stati differenti, si sarebbero avute 6 tensioni incognite (ai vertici A1... B3) e 6 equazioni che le contenevano. Ciascuna equazione avrebbe indicato che la somma di tutte le correnti che fluiscono in un dato spigolo deve eguagliare la somma di quelle che ne fuoriescono, con le correnti ottenute dalla legge di Ohm I=ΔV/R. (Se non si è sicuri se il flusso è entrante o uscente, se ne indichi un verso; si potrà ottenere un meno da qualche parte, ma è OK). Ciò può richiedere un sacco di lavoro in più! Rompicapi(1) Quanto vale R se si aggiunge ancora un resistore di 1 Ω , tra A2 e A3?Risposta Nel cubo appena studiato, A2 e A3 hanno entrambi la stessa tensione, cioè V1. Se li collegassimo mediante un qualsiasi resistore (di qualunque valore), nessuna corrente lo attraverserebbe, perché entrambe le estremità si trovano alla stessa tensione. Quindi R rimane lo stesso, 5/6 Ω Questo suggerisce che il problema potrebbe essere risolto anche più velocemente con un trucco basato sulla sua simmetria. Siccome (A1,A2,A3) si trovano tutti alla stessa tensione, noi potremmo anche collegarli mediante un filo di resistenza trascurabile, in modo che nel circuito elettrico si trovino allo stesso punto – chiamiamolo "C". Analogamente (B1,B2,B3) si trovano alla stessa tensione, possono anche essere collegati direttamente ed essere elettricamente lo stesso punto del circuito – chiamiamolo "D". Con queste scorciatoie:
Da A a C : tre resistori da 1 Ω in parallelo, equivalenti a R1 = 1/3 Ω
(2) Si supponga che i tre resistori da 1 Ω tra A e (A1,A2,A3) vengano sostituiti con resistori da 2 Ω . Ora quanto vale R?
L'equazione (2) di cui sopra ora cambia in
Le altre equazioni rimangono le stesse. Si sommi come prima La resistenza equivalente è perciò 7/6 Ω. Usando la scorciatoia descritta sopra, R1 = 2/3 Ω e si ottiene lo stesso risultato. |
