Plan du Site

(11a) Ellipses et première Loi de Kepler

Comme il a déjà éténoté, il y a d'autres façons de repérer les points d'un plan. Par exemple, un point P peut être déterminépar sa distance r à un point central O ("origine") et l'angle f (ou Grec φ) entre la droite OP et une certaine direction standard, "d'origine". Ces "coordonnées polaires" (schéma) sont les plus adaptées pour décrire le mouvement planétaire.

L'ellipse en coordonnées polaires

On sait que si toutes les valeurs de (r,f) d'une courbe sont reliées par une certaine équation, qui peut être symboliquement écrite

r = r(f)

la fonction r(f) est l'équation de la courbe, en coordonnées polaires. La fonction la plus simple est un nombre constant a, donnant la courbe

r = a

La valeur de r vaut a pour n'importe quelle valeur de f. Cela donne un cercle autour de l'origine, de rayon égal à a, (schéma ci-dessus).

l'Ellipse

Considérez maintenant cette courbe, dont l'équation est

r = a(1- e²)/(1+ e cos f)

où e est l'excentricité, un nombre entre 0 et 1

Si e = 0, on a évidemment le cercle déjà vu

Mais pour les autres valeurs ?

La fonction cos f présente un comportement ondulatoire (illustration ci-dessous), et tandis que f parcourt un cercle complet, elle diminue de +1 à 0, puis à -1, puis augmente à nouveau à 0 et à +1.Donc, le dénominateur de l'équation monte et descend comme une vague. Il est minimum quand cos f = -1 . Voici la table des valeurs principales (360 est entre parenthèses, parce qu'elle représente la même direction que 0 degrés):

f degrees	0	90	180	270	(360)
cos f	1	0	-1	0	1
1 + e cos f	1 + e	1	1 - e	1	1 + e

Même si e est plus petit que 1, le dénominateur de la fonction reste toujours positif. Il n'est jamais égal à 0 , si bien que pour n'importe quelle valeur de f, il y a toujours un r correspondant. En d'autres termes, la courbe reste toujours à distance de son origine, elle est fermée.

L'expression (1 - e²) peut être mise en facteurs, c'est-à-dire écrite comme deux expressions multipliées l'une par l'autre ("le produit de deux expressions"). Comme expliquédans la section sur les identités algébriques .

1 - e² = (1 - e)(1 + e)

A certains points sur la table ci-dessus, soit (1-e), soit (1+e), élimine le dénominateur et en simplifiant l'équation entière, on obtient:

f degrees	0	90	180	270	(360)
r	a(1 - e)	a(1 - e²)	a(1 + e)	a(1 - e²)	a(1 - e)

Ainsi, la distance des points de la courbe à l'origine oscille entre a(1-e) et a(1+e), et le résultat est un cercle aplati ( une ellipse) dont le point O (l'origine) est un foyer. Toutes les orbites planétaires ressemblent à des ellipses ayant chacune sa propre excentricitée. Plus e est petit, plus la forme est proche du cercle. L'orbite de la terre est très proche du cercle, avec e = 0.0168, et les autres principales planètes (exceptéPluton) ont des excentricités comparables : sur un schéma respectant les dimensions de ces orbites, l'oeil ne peut pas faire la différence avec un cercle. Pour l'orbite de la comète Halley, e est d'autre part tout à fait proche de 1.

L' ensemble des points pour qui
R1 + R2 ont la même valeur est une ellipse

Comme mentionnédans la section précédente, un deuxième foyer O' peut être dessinésymétriquement à O, et l'ellipse peut être définie (en réalité, c'est sa définition originale,) comme la collection de points pour lesquels la somme R₁+R₂ de leurs distances à O et O' est la même :

La plus longue dimension de l'ellipse, la distance A B , suivant la droite reliant les deux foyers, est son "Grand Axe." Si (R₁,R₂) sont sur cet axe, ils représentent les distances des foyers O et O' à A, alors R₁ = OA = a(1+e), la plus petite distance de l'ellipse et R₂ = O'A = OB (par symétrie) est la plus grande distance et égale donc a(1+e). Mais, OA + OB = AB, par conséquent :

AB = a(1 - e) + a(1 + e) = 2a

Il en découle que la quantitéa est connue dans l'équation de l'ellipse comme demi grand axe. Nous pouvons maintenant préciser la loi de Kepler comme "Le carréde la période orbitale T est proportionnelle au cube du demi grand axe a de son orbite autour du soleil."

Les deux quantités (a,e) définissent complètement l'ellipse. Quand cette ellipse est l'orbite d'une planète ou d'un satellite, elles forment deux des six éléments orbitaux qui définissent l'état du corps en orbite. Un troisième élément, l'anomalie moyenne M, indique la position de la planète ou du satellite sur son orbite, et les trois autres restants définissent l'orientation de l'orbite dans l'espace à trois dimensions. Des précisions au sujet des éléments orbitaux seront données dans la section (12b).

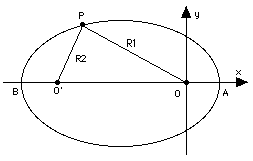
Précisions sur la première loi

La première loi de Kepler :"l'orbite d'une planète est une ellipse, avec le soleil à un foyer" n'est pas exacte à 100%.

Imaginez que, par magie, la planète devienne de plus en plus lourde, et le soleil de plus en plus léger. À un certain point, les deux auraient le même poids: pourrions-nous alors dire lequel orbite autour de l'autre ?

Pour être très précise, la première loi devrait placer le foyer de l'ellipse orbitale au centre de gravité du système planète - soleil. (Le centre de gravitésera défini plus tard, mais intuitivement, si les masses sont très inégales, comme pour une planète et le soleil, il se trouve près du centre de l'objet plus lourd.) Puisque le soleil est beaucoup plus lourd que Mars, l'effet sur l'orbite de Mars, que Kepler a étudié, était trop petit pour être perçu. Néanmoins, le soleil se déplace aussi sous l'influence de ses planètes, et ce type de mouvements est devenu un outil important pour la recherche de planètes, en dehors du système solaire.

Une planète, comparable à la terre, satellite d'une étoile éloignée, serait trop lointaine et trop sombre pour être vue avec les télescopes terrestres, surtout à proximitéde la lueur de l'étoile, son soleil. Cependant, la planète circule sur une orbite, mais son étoile se déplace également sur une orbite, en image miroir- autour d'un centre de gravitécommun, c'est une orbite beaucoup plus petite, avec un mouvement beaucoup plus lent, parce que le centre de gravitéest très proche du centre de l'étoile (dans le système Terre - Soleil, il est même à l'intérieur du soleil), mais qui peut quand même être détectépar des variations subtiles de luminosité.

Récemment de telles planètes ont étédécouvertes, mais la plupart ressemblent à Jupiter et aucune ne semble appropriée à la vie. La recherche continue cependant. (Vous pouvez découvrir son état actuel (et beaucoup plus) sur le site web de "recherche de planète" Planet Quest du laboratoire du Jet propulsion Lab de la NASA (JPL).) Une découverte récente (15 avril 1999) a étéle système de upsilon Andromeda qui semble contenir au moins 3 planètes. (Pour une autre découverte récente associée à une planète éloignée, cliquez ici.)

Les corps du système solaire peuvent également se déplacer selon d'autres sections coniques, paraboles ou hyperboles, dont les équations ressemblent à celle d'une ellipse, mais avec e égal ou supérieur à 1. Strictement parlant, ces orbites n'ont pas "de demi grand axe," parce qu'elles n'ont pas de limites en taille comme les ellipses mais se prolongent à l'infini.

Il faut alors écrire :

r = p/(1 + e cos f)

ce qui ne pose pas de problème si e=1 : Ces corps ne sont pas liés au soleil, et sont libres de lui échapper. Le dénominateur dans l'équation de la trajectoire s'annule pour quelques valeurs de f, rendant son r infini, et lorsque que le corps mobile approche ces valeurs, il se déplace au loin, sans limite. En général les comètes ont une excentricitée proche de 1, ce qui veut dire qu'elles sont venues des limites extrêmes du système solaire. La sonde spatiale Voyager 2, dont e>1, est sur le point de sortir du système solaire, pour n'y plus jamais revenir.

Prochaine étape: #12 Seconde Loi de Kepler

Revenir à la liste principale

Chronologie et Glossaire

Auteur et responsable : Dr. David P. Stern
Mail au Dr .Stern: stargaze("at" symbol)phy6.org
Traduction française: Guy Batteur guybatteur(arobase)wanadoo.fr

Dernière mise à jour : 12.23.2003