|
La conversion des protons en neutrons résulte d'une autre
force nucléaire, la "force faible " (le
mot «nucléaire» est ici sous- entendu).
La force faible agit aussi à courte distance, mais est
beaucoup plus faible que la force forte
La force faible tend à rétablir
l’égalité de nombre entre neutrons et
protons dans le noyau, ces deux particules, étroitement
liées, étant parfois appelées
collectivement nucléons
Les protons ne se combinent à l'hélium que
s’ils ont acquis suffisamment de vitesse
pour vaincre leur répulsion réciproque et ainsi
obéir à l’attraction
forte nucléaire, ce qui signifie qu'ils doivent former un
gaz très chaud. Il faut une pression
énorme pour maintenir la chaleur nécessaire
à la combinaison de l’hydrogène en
hélium, ce qui est le cas des régions centrales
du soleil ( "coeur"), en raison de l'énorme poids
des couches sus-jacentes, du à la forte gravité
du Soleil.
Le processus de combinaison des protons pour former l'hélium
est un exemple de fusion nucléaire.
Nos océans regorgeant d’hydrogène et
l'hélium - non nuisibles à l'environnement -, il
serait idéal que les physiciens puissent maîtriser
la fusion nucléaire pour alimenter le monde en
énergie. Les expériences en ce sens
n’ont jusqu'à présent guère
abouties. On a utilisé de l’hydrogène
assez chaud pour être ionisé, et de
très puissants champs magnétiques pour l'isoler
, (puisque les
particules chargées "s' accrochent" aux lignes de champ
magnétique, comme celles
piégées par la ceinture de radiations de la
Terre). Ces expériences de fusion concernent aussi
l'hydrogène lourd, qui fusionne plus facilement, avec une
densité de gaz modérée.
Malgré toutes
ces astuces, on a bien obtenu une énergie de fusion, mais
pour ce résultat, il fallait encore un surplus
d'énergie.
La
courbe de l'énergie de liaison
Le nombre de
neutrons égale celui des protons pour
les principaux isotopes des atomes aux noyaux
légers, comme le carbone, l'azote et l'oxygène,
Mais avec des noyaux plus lourds, l’énergie
perturbatrice des protons augmente, car ils sont
confinés dans un petit volume et se repoussent les uns les
autres. L'énergie de la force forte, celle qui maintient la
cohésion du noyau, augmente parallèlement, mais
à un rythme plus lent, comme si dans le noyau, seuls les
nucléons les plus rapprochés les uns des autres
restaient étroitement liés, et pas les
autres, plus éloignés.
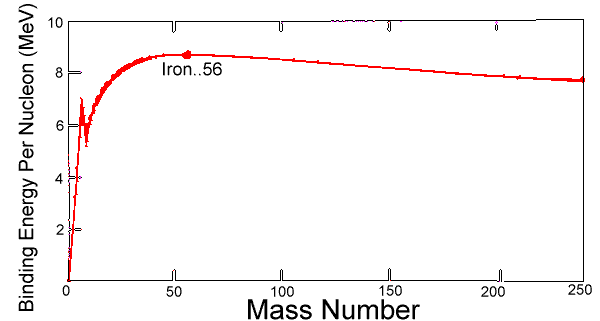
Le bilan de
l’énergie de liaison
d'un noyau est celui de l'attraction intranucléaire, moins
les perturbations dues à la
force
d’énergie électrique. Lorsque les
noyaux deviennent plus lourds que celui de l'hélium, leur énergie
de liaison par nucléon (déduite de la
différence de masse entre le noyau et la somme des masses
des nucléons composants) augmente mais de plus en plus
lentement,
jusqu’à atteindre un maximum avec le fer.
Avec encore plus de nucléons, l'énergie de
liaison nucléaire continue bien à
augmenter - mais le total des forces
perturbatrices de l'énergie électrique (protons
positifs repoussant les autres protons) augmente encore plus, et
devient prépondérante.
On peut donc dire que le noyau de 56
Fe est le plus efficacement lié. (voir
référence #10b)
Grâce à la force faible, le nombre de neutrons
dépasse celui des protons, réduisant ainsi les
perturbations d'énergie - par exemple, dans
l’isotope principal du fer, 26 protons, mais 30 neutrons.
Bien sûr, il y a aussi des isotopes au nombre de
neutrons différent, mais s' ils sont trop loin de
la stabilité, les nucléons se convertissent
après un certain temps en un isotope stable par
émission de beta radioactivité --les
protons se transformant en
neutrons par absortion d' un électron (ou
émission d' un positon,
la contrepartie positive de l'électron), ou
inversement les neutrons
deviennent des protons en émettant des électrons.
Avec les noyaux plus lourds, composés de plus de 200
nucléons, les forces électriques peuvent
être si déstabilisantes qu’une partie
entière du noyau est éjectée,
généralement par combinaisons de 2 protons et 2
neutrons (rapides ("particules alpha ,"
», donc en fait des noyaux d'hélium),
extrêmement stables. La courbe d'énergie
de liaison (dessin) avoisine l’énergie
de liaison par nucléon, proportionnellement à la
masse atomique. Elle s’amplifie jusqu’au niveau du
fer puis rediminue lentement,présentant aussi un pic au
niveau de
l'hélium, très stable comme on l'a vu. Dans la
nature, les noyaux
les plus lourds, ceux de l'uranium 238U
, sont instables, mais comme leur durée de vie est de 4,5
milliards d'années, proche de l'âge de la Terre,
ils restent relativement nombreux. Ils pourraient provenir
d’une
explosion de supernova
(référence #8)
ayant précédé la formation du
système solaire. (et de même pour d'autres
noyaux plus lourds que le fer)
L’isotope le plus fréquent du thorium,
232T , émet aussi des
particules α, et sa demi-vie ( temps
pendant lequel la moitié des atomes se
désintègre) est encore plusieurs fois plus
longue. Dans les deux cas, la désintégration
radioactive produit des " isotopes –filles » ( NDLT
: fils ?),
également instables, qui entament une chaîne de
désintégrations se terminant par un isotope
stable.
Pour le plaisir
:
Le livre " The Curve of Binding Energy " de John McPhee est en
réalité
l'histoire de Théodore Taylor, physicien
nucléaire aux multiples sujets
d’intérêts.
Problèmes
( Réponses en section S-8A-5)
(1)
Pourquoi ne peut-on trouver dans notre environnement des
éléments dont les atomes pèsent 300
fois
plus que le proton, ou plus?
(2)
Etablir un glossaire définissant brièvement par
ordre alphabétique, dans vos propres termes :
radioactivité alpha, bêta
radioactivité, énergie de liaison, fusion
nucléaire contrôlée, coeur du Soleil,
courbe de liaison d'énergie, isotopes - fille (fils),
deutérium, spectromètre de masse, fusion
nucléaire, positron, force nucléaire faible,
force nucléaire forte.
(3)
Quelle est la source de l'énergie solaire?
(4)
Pourquoi donne-t-on à l'énergie de liaison du
noyau un signe négatif ?
(5)
(a)
La masse atomique du
deutérium (22
H) est 2.0140, de l'hélium 4 He
4.0026 (en unités de masse du proton), et
"l'énergie au repos" E=mc2
du proton est 938,3 MeV ( millions d'eV, avec 1
eV = un électron-volt; voir #9).
Combien d'eV
sont- ils libérés quand deux atomes de deuterium
se
combinent par fusion nucléaire en un 4
He ?
(b) Si 1 eV = 1.60 10–23
joule et le nombre d'Avogadro A = 6.022 1023, combien de joules sont
libérés par la fusion de 4 g de
deutérium?
(c) Un gramme de TNT peut
libérer 3,8 kilocalories d'énergie,
l'équivalent de 4184 joules. Combien de tonnes de TNT
sont-ils
nécessaires à la libération de
l'énergie calculée ci-dessus?
(6)
Voici une autre application de l'équation d'Einstein E=mc2
.Il vaut mieux se familiariser avec la notation scientifique pour les
très petits et très grands nombres avant
d'essayer de résoudre ce problème, et
vérifiez toutes les étapes du calcul.
Le Soleil perd sans cesse de la masse, au moins de deux
façons différentes.
D'abord, par irradiation de
l’énergie E de sa lumière, ce qui
réduit également sa masse, en raison de
l'équivalence de l'énergie et de la masse.
L'énergie rayonnée au niveau de l'orbite de la
Terre – à 150 millions de kilomètres du
Soleil - est d'environ 1300 watts (" la constante solaire")
par mètre carré de surface perpendiculaire aux
rayons du soleil, et la vitesse de la lumière est c = 300000
km / sec.
Ensuite, par émission du vent
solaire.
Pour des raisons qui depuis 70 ans ne sont pas encore claires, la plus
haute atmosphère du soleil ("couronne solaire")
est très chaude, environ un million de degrés
centigrades, ce qui explique pourquoi les atomes de cette couche ont
tendance à être dépouillés
de la plupart ou de la totalité de leurs
électrons - -par exemple des atomes de fer à qui
il manque une douzaine d'électrons, ce qui exige une
énorme quantité de pertubations.
La gravité du Soleil ne peut pas retenir un gaz aussi chaud.
Par contre, la plus haute atmosphère solaire est constamment
balayée par le vent solaire --un
courant raréfié d'ions et d'électrons
libres, éjecté à environ 400 km /
seconde. La densité de ce vent au niveau de l'orbite de la
Terre est d'environ 10 protons / centimètre cube (en tenant
compte de la présence d'ions d'hélium), et la
masse d'un proton est d'environ 1.673 10–27
Kg.
Quel est de ces deux processus le responsable de
la plus grande perte de masse du Soleil ?
(7) Pour qu’un objet (par
exemple, un vaisseau spatial) soit éjecté de la
surface de la Terre, il lui faut une vitesse v1
=
11.3 km/s
pour s' échapper à la gravité
terrestre
("vitesse d'échappement").
L'énergie au repos d’un neutron vaut E0
= mc2
= 939.535 MeV (millions d'électrons-volts). Lla vitesse de
la lumière est de 300.000 km / sec (pratiquement) et si un
neutron est éjecté de la surface de la terre avec
juste assez de vitesse pour échapper à la
gravité, quelle est l'énergie en MeV (ou en
électrons-volts, eV)? Utilisez une expression non
relativiste basée sur l'énergie
cinétique E1 des neutrons
s’échappant (c’est suffisamment
précis). |