#21b     Vuelo a Marte: ¿Cuánto durará?
¿Por dónde ir?

    Usando la mecánica orbital desarrollada anteriormente, podemos ahora planear (con aproximaciones) una misión espacial a Marte. Asumiendo que tenemos el propulsor y la nave, ¿como deberían ser dirigidos, y cuánto tiempo llevaría el vuelo?.

    Como aproximación, supongamos que la órbita de la Tierra y de Marte son ambas círculos en el mismo plano, centradas en el Sol. El radio de la órbita terrestre, indicado por r₁, es de alrededor de 150.000.000 kilómetros, una distancia conocida como unidad astronómica (UA). Es una unidad conveniente para medir distancias en el sistema solar y fue usada en la sección #10 sobre las leyes de Kepler. Como en esa sección, aquí tambien todas las distancias serán medidas en UA y los tiempos en años. Con tales unidades, para r₁ de la Tierra = 1 UA y el período orbital es T₁ = 1 año. Para Marte (subíndice 2), r₂ = 1,523691, T₂ = 1,8822.

    Nota: Todas las cantidades en esta sección y en la siguiente son, o bien no-vectores, o magnitudes de vectores. Cuando una cantidad está en negrita, es solamente por claridad y no lleva ninguna connotación de que sea un vector.

Cómo no ir

La Tierra y Marte en su situación más próxima.

    Aquellos que no están familiarizados con órbitas podrían pensar que la mejor manera de llegar a Marte desde la Tierra es esperar a que los dos planetas estén cerca uno del otro (como muestra la figura), luego dirigir el cohete hacia Marte y lanzarlo. Así es como supuestamente se hace en "La Guerra de los Mundos" por H.G. Wells, aunque en esa historia se usa un cañón gigante, no un cohete, y el disparo va en la dirección opuesta, es decir, de Marte a la Tierra. Eso no funcionaría (en ninguna dirección) por varias razones.

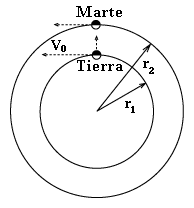
    Primero, la gravedad de la Tierra doblaría la trayectoria de cualquier nave espacial lanzada desde aquí. Para quitar ese factor, asumamos que el cohete ha sido ya ubicado en una órbita distante alrededor de la tierra, donde la gravedad de la Tierra es débil y el movimiento orbital lento, permitiendo que sean despreciables. En la planificación real de la órbita deberían tomarse en cuenta como una corrección.

    Aún así, ese cohete está orbitando el Sol junto con la Tierra, a la cual sigue ligeramente unido, moviéndose a aproximadamente 30 km/seg, una velocidad que escribiremos como V₀. Esta es mucho más rápida que la que necesitamos para alcanzar la órbita de Marte (¡o que la que se puede alcanzar fácilmente con los cohetes!). Si arrancamos los motores cuando Marte está más cerca (figura), V₀ es transversal a la dirección del objetivo, de modo que la nave espacial arrancará en una dirección bastante diferente a la que apunta a Marte (suma de vectores) y es seguro que Marte se habrá movido mucho, antes de que ésta (la nave) haya cubierto la distancia intermedia. Esta es la segunda razón.

    La tercera razón es que el sistema entero está dominado por la gravedad del Sol. Todos los objetos viajan en órbitas o trayectorias, las cuales, por las leyes de Kepler, son parte de secciones cónicas, elipses en este caso. En general, éstas trayectorias están curvadas.

Órbita de transferencia

    Por lo tanto, en lugar de "apuntar y disparar", es mejor buscar una órbita que lleve la nave espacial de la Tierra a Marte, y decidir el lanzamiento cuando la llegada a la órbita de Marte coincida con el arribo de Marte a la misma ubicación.

La órbita de transferencia de Hohmann

    Además, la dirección en la cual la nave espacial se mueva cuando llegue a Marte, debería facilitar la igualación de su velocidad con la de Marte. Esto nos lleva a la llamada Elipse de Transferencia de Hohmann (u órbita de transferencia), presentada por primera vez en 1925 por el Ingeniero alemán Wolfgang Hohmann. Esto es, una elipse con perihelio P (el punto más cercano al sol) en la órbita de la Tierra, y un afelio A (punto más distante del Sol) en la órbita de Marte (figura). Una elipse de transferencia similar, entre la órbita baja de la Tierra (digamos, r = 1,1 RE = 1,1 veces el radio de la Tierra) y la órbita sincrónica a 6,6 RE (ver sección #21a) es usada frecuentemente para inyectar satélites de comunicación en sus órbitas finales. Nosotros lanzamos desde P, dándole al cohete una velocidad adicional además de V₀, inyectándolo así en la elipse más grande.

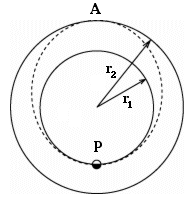
    Marte debería estar en una posición tal, relativa a la Tierra en el momento del lanzamiento, que alcanzase el punto A al mismo tiempo que la nave espacial. Para determinar esa posición necesitamos saber la duración del vuelo desde P hasta A, y ésta se deduce más abajo, usando la 3ª ley de Kepler.

3ª Ley de Kepler

    La 3ª ley de Kepler usada aquí tiene la misma forma que en la Sección #10. Para mantener la unidad, esa forma la deducimos nuevamente más abajo. La ley afirma que, para todos los objetos que orbitan el Sol, se cumple que:

T² / a³ = constante

    donde T es el período orbital y a es el semieje mayor, la mitad del diámetro mayor de la elipse orbital (a=r en órbitas circulares). La constante es la misma para todos los objetos orbitando el Sol, incluyendo por supuesto la Tierra. Su valor exacto depende de la unidad en la cual midamos T y a. Ese valor resulta ser muy simple si T se mide en años, y a en UA (como hemos hecho aquí). Insertando la ecuación de la 3er ley el valor para la Tierra da

T = 1 (año)                     a = 1 (AU)

    en nuestras unidades, entonces

T² / a³ = 1

    Consecuentemente, en estas unidades la constante también iguala a 1, y el valor puede ser usado para cualquier planeta. Multiplicando ambos lados de la ecuación por a³ (segunda ley del álgebra)

T² = a³

    Esto también se mantiene para cualquier órbita alrededor del Sol, incluyendo la de una nave espacial en una elipse de transferencia. La longitud de esa elipse es, en UA,

r₁ + r₂   =   1 + 1,523691   =   2,523691 UA

    Ese es el eje mayor de la elipse orbital, y la mitad de su longitud iguala al semieje mayor a . Por lo tanto

a = 1,261845                         a³   =   2,00918   =   T²

    Tomando la raíz cuadrada

T   =   1,417454 años

La Tierra y Marte en el     momento del lanzamiento

    Ese es el tiempo para ir desde P hasta A y volver a P. El tiempo de viaje hasta Marte es la mitad de eso, es decir 0,70873 años o aproximadamente 8,5 meses.

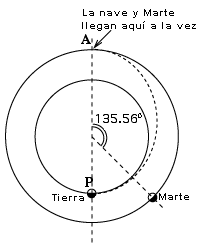
Ubicación de Marte

    ¿Dónde debería estar Marte en el momento del lanzamiento? De acuerdo a las cifras mencionadas al comienzo de esta sección, Marte tarda 1,8822 años para completar una órbita de 360° Por lo tanto, suponiendo una órbita circular y movimiento uniforme (una aproximación que es menos exacta para Marte que para la Tierra), en 0,70873 años debería cubrir

360° * (0,70886 / 1,88) = 135,555°

    Por lo tanto, lanzaríamos cuando Marte en su órbita estuviera a 135,555° de distancia del punto A (dibujo).

    En la próxima sección se calcula la velocidad que debe impartirse al cohete en el punto P para producir la órbita de transferencia, y el cambio de velocidad requerido en el punto A para igualar la velocidad de Marte. Este cálculo es más largo y requiere algo de álgebra.