|
in Orbit Electric Forces |
With only the simplest equipment, you too can perform mass measurements similar to the ones aboard Skylab.
|
|
|
in Orbit Electric Forces |
With only the simplest equipment, you too can perform mass measurements similar to the ones aboard Skylab.
|
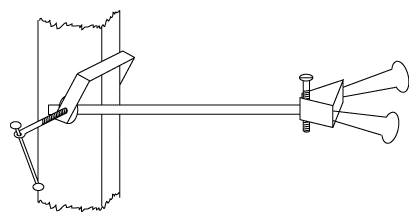 |
Instructions
|
|
The theory predicts that the oscillation period should be proportional to the square root of the oscillating mass, including the mass of the clip. Note that gravity plays no part here: the oscillation period would be the same on the Moon or in zero-g. Denoting square root by SQRT, we have
|
|
(T2/T1) = SQRT(m2+m0)/SQRT(m1+m0) = SQRT[(m2+m0)/(m1+m0)].
|
|
("The ratio of square roots is the square root of the ratio"). Muliplying each side by itself: (T2/T1)2 = (m2+m0)/(m1+m0). If we were in space, measured T1 and T2, and knew the masses m1 and m0, then we could calculate an unknown mass m2.
|
|
Weights: m1 = 50 gr, m2 = 120 gr, m0 = 10 gr. The number of oscillations counted in a 10-second period was: with m1, 20 oscillations, with m2, 13.5 oscillations. Then
|
|
T1 = 10 sec/20 = 0.5 sec T2 = 10 sec/13.5 = 0.74074 sec. so that
(T2/T1)2 = 2.195 should equal (m2+m0)/(m1+m0) = 130/60 = 2.167 |
|
This agreement is probably better than such a crude experiment deserves, considering that the mass of the sawblade itself was ignored.
|
Next Stop: #18 Newton's Second Law
Timeline Glossary Back to the Master List
Author and Curator: Dr. David P. Stern
Mail to Dr.Stern: stargaze("at" symbol)phy6.org .
Last updated: 9-21-2004
Reformatted 24 March 2006