(17) Mass

    Even on Earth gravity isn't the same everywhere! Newton already knew that on Earth the effective weight of an object was slightly smaller on the equator, due to the Earth's rotation. He was aware that if a pendulum clock--using gravity--was accurate in England, it ran slow after being moved to the equator. Portable clocks using a balance wheel, which rotated back and forth against a spring, did not have this problem. Such clocks used inertia, and they ultimately evolved into the accurate "chronometers" by which ships navigated (read "Longitude" by Dava Sobel).    

Still, the easiest and most common way of measuring mass is by weighing, which uses gravity. In a two-pan balance, we compare the weight of an unknown object to that of a set of known weights: Because of this, mass is usually measured in kilograms, even though these are also units of weight. In a one-pan balance, like the one pictured here, the comparison weights are fixed, but by sliding them to different distances from the pivot, the same result is achieved.

Measuring Mass on a Space Station

    In 1973 NASA put in orbit the space station Skylab, and its experiments included a careful monitoring of the health of the crew. One important quantity was the body mass of the astronauts. Here on Earth it would be called "body weight" and would be measured by weighing a person on scales. However, scales would not work on a space station. They use gravity, balancing its force on the astronaut's body against a calibrated spring or against the force of gravity on some calibrated weights.

    It is not correct to say that gravity does not exist on an orbiting spacecraft (if it did, the spacecraft would fly away, never to return). Rather, in the "zero g" environment of the space station, gravity is already doing all it can in moving the station in its orbit, and none of it is evident inside the station. Since the orbit is curved, the first law is not violated by requiring a force to maintain it.

How can mass be measured there?

    One gets a clue from clocks, all of which need some sort of device that gauges the passage of time. Pendulum clocks--always kept upright--use gravity, but mechanical wristwatches depend on a balance wheel, turning periodically back and forth--clockwise, then counter-clockwise, then clockwise again--against a spiral spring. Gravity is not involved. Modern electronic wristwatches replace the wheel with a vibrating quartz crystal, acting somewhat like a tuning fork: the motion is much faster, but transistor circuits can easily count the vibrations, which are very stable.

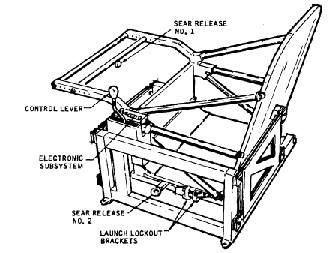
    The frequency of the balance wheel--its number of back-and-forth oscillations--depends on its rotational inertia. Astronauts aboard "Skylab" used something similar--but with a simpler back-and-forth motion, rather than a rotation. It resembled a porch glider, a seat which could glide forward and back against springs (see drawing above).

    Since the oscillation is opposed by inertia, the greater the mass, the slower is the process, and by measuring the frequency of oscillation, a fair idea of body mass could be obtained. For further details on mass measurements aboard "Skylab," see the next section.

Lorand Eötvös

        Optional:

Gravitational Mass and Inertial Mass

You will notice that the mass of an object can be measured (that is, compared to the mass of one liter of water) in two different ways. Some physicists accordingly distinguish gravitational mass m_g from inertial mass m_i. Using scales and the local force of gravity, one can determine gravitational mass; or else, one might dispense with gravity, like the astronauts aboard Skylab, sand measure the "inertial mass," and in principle they may differ.

One could imagine a universe where the two are not proportional (whenever they are proportional, a choice of units can make them equal). In that universe a chunk of lead may have (as in our own universe) about 4 times the weight of a chunk of aluminum of the same size and shape, but only twice the inertia. Two-pan scales will give the chunks weights with a ratio 4:1, but devices like the ones of the sections that follow will only give a mass ratio 2:1.

As it happens, our own universe is not like this, but the two masses are always the same. Around 1900 the Hungarian physicist Roland Eötvös (Lorand in Hungary; see picture) compared the two, using extremely sensitive instruments. He concluded that they were the same to an accuracy of many decimals, and that equality became one of the foundations of physics, especially of the general theory of relativity. Some years ago it was suggested that a small difference existed, hinted by small differences in results by Eötvös for different substances (even though the variation he found was within error bounds). This lead to a search for a "5th force" modifying gravity, but careful measurements disproved the existence of such a force.

---

Questions from Users: ***  

What if you could lose weight without losing mass? A century ago H.G. Wells wrote a humorous and delightful fantasy story around this possibility, The Truth about Pyecraft.. Look it up!