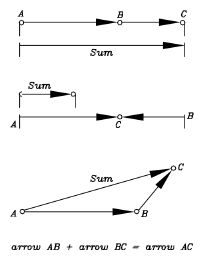
 So far this is just a complicated way of doing something obvious. What makes "arrow addition" useful is that it also holds when directions are different. Suppose the airplane flies into a headwind of 100 mph: we expect the velocity relative to the ground to be
200 - 100 = 100 mph
So far this is just a complicated way of doing something obvious. What makes "arrow addition" useful is that it also holds when directions are different. Suppose the airplane flies into a headwind of 100 mph: we expect the velocity relative to the ground to be
200 - 100 = 100 mph
and the "arrow addition" confirms it (middle figure, lengths distorted).
Next suppose the pilot's course is eastwards, but a 100 mph cross-wind blows towards the north-east: in what direction does the airplane move, and how fast? Intuition does not help, but arrow addition does (bottom figure, not to scale).
The general rule is, the combined velocities bring the airplane in an hour to the same spot as when first one motion, then the other, acts alone for an hour. As expected, the direction is somewhere between eastward and northward.
All vectors can be added together in this way--like arrows, head to tail. There exists an alternate method, though, often easier to use, and it is described next.
Resolving vectors into components
Just as one can combine two vectors into one--their sum--so it is also possible to move in the opposite direction--given a single vector, find two vectors whose sum it is.
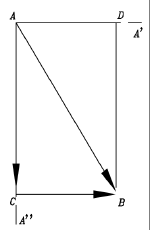 Suppose the given single vector is represented by the arrow AB in the drawing, and we wish to resolve it into the sum of two vectors directed along AA' and AA". We draw lines along AA' and AA" and also lines parallel to them from B, the other end of the vector. If AA' and AA" are perpendicular to each other (the usual case), then these lines enclose a rectangle ACBD, of which AB is a diagonal. It is now evident that AC and CB are a solution to our problem, and in vector addition
Suppose the given single vector is represented by the arrow AB in the drawing, and we wish to resolve it into the sum of two vectors directed along AA' and AA". We draw lines along AA' and AA" and also lines parallel to them from B, the other end of the vector. If AA' and AA" are perpendicular to each other (the usual case), then these lines enclose a rectangle ACBD, of which AB is a diagonal. It is now evident that AC and CB are a solution to our problem, and in vector addition
AC and CB are called the components of AB (or component vectors of AB) along the two given directions. AD and DB, which have the same length and direction, are also a solution and represent the same components, the difference being their addition is performed in reverse order. If AA' and AA" are not perpendicular, then ACBD is a parallelogram.
The Uses of Component Vectors
Resolving vectors into components can be very useful. Three examples are given below and more follow in section (22a).
(a) Adding many vectors
Suppose it is required to add 10 vectors (yes, situations exist...). To perform it the way described earlier, one adds the first two vectors head-to-tail, then adds the third to their sum, then the fourth... tedious business!
A faster way is to choose two perpendicular directions, and taking our cue from cartesian coordinates, one will be named here "the x direction" and the other "the y direction". Resolve each vector V into an "x component" Vx along the x direction and a "y component" Vy along the y direction.
Now we have not 10 but 20 vectors which need to be added up, but the job is much easier. Of those vectors, 10 are lined up with the x-direction, and vectors in the same direction (like head- and tail-wind velocities in the earlier example of the airplane) add up like ordinary numbers. The same goes for the 10 vectors lined up with the y-direction. The problem is now reduced to two strings of ordinary additionas and subtractions (oppositely directed vectors have minus sign), and only the last step--adding together the grand totals in the x and y directions--requires vector-type addition.
Note: The real world is three dimensional, and so are its vectors. But 3-D vectors can also be resolved, each of them equal to the sum of three vectors in the (x, y, z) directions (the rectangle now becomes a rectangular box). Components of the same kind are added as in the 2-dimensional example above, and the final addition just involves one sum-vector in each dimension. The vector sum is now the diagonal of the rectangular box of which the three sums are the sides.
(B) Calculating a vector sum
The head-to-tail addition of vectors allows one to construct their sum graphically. Components allow it to be calculated. A notation describing vectors is easily obtained: a vector with components A in the x-direction and B in the perpendicular y-direction can be represented as (A, B), by two numbers sharing parentheses.
[The values of (A,B) can change if the same vector is represented in different coordinates, but that is just its representation mode. Similarly, a temperature is the same if represented in degrees centigrade or farenheit, although the numbers representing it may differ.]
Take the earlier example of vector addition--an airplane flying east at 200 mph (its airspeed, its velocity relative to the air), while a 100 mph wind blows towards the north-east. The vector addition triangle of this example is at the bottom of the first figure of this section.
Let the x-direction be eastward and the y-direction northward. Then the (x,y) velocity components are, in mph,
- --of the airspeed, (200,0)
- --of the wind velocity (100 cos 45o,100 sin 45o) = (70.7, 70.7)
since cos 45o = sin 45o = 0.707 (derived here). Thus the total velocity components are
(Vx,Vy) = (200+70.7,0+70.7) = (270.7,70.7)
This gives the total velocity V. By the theorem of Pythagoras,
V2 = (Vx)2 + (Vy)2
giving the magnitude of V as approximately 280 mph, while the sharp angle at point A in the figure (we will name it A, too) satisfies
sinA = 70.7/280 = 0.2527
From which A is about 16.25 degrees.
(c) The Inclined Plane
This goes back to Galileo's experiment. Suppose we have a smooth incline sloping at an angle s (drawing below) and on it a well-greased block, ready to slide down (Galileo used a rolling ball, with which the experiment is easier to perform but harder to calculate, since the kinetic energy is now divided between that of the sliding motion and the one of rotation). If friction is negligible--how fast will the block slide?
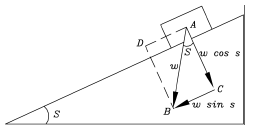
The force of gravity on the block--it has a name, it is called the block's weight W--can be represented by a vertical arrow AB of length W, pointing straight down. That is not the direction in which the block can accelerate. However, the vector AB can also be resolved into two mutually perpendicular forces:
- One is perpendicular to the surface, is represented by the line AC and has magnitude W cos s. That force is completely cancelled by the resistance of the surface, which allows no motion in that direction. If the motion includes friction, however, the force of friction is proportional to this component.
- The other force is parallel to the surface, is represented by the line AD, has magnitude W sin s and, if no friction impedes the motion, is free to accelerate the block in that direction. The force is smaller that the weight W by a factor (multiplier) sin s, a number always smaller than 1, while the mass of the block is unchanged. Its acceleration is therefore reduced by a similar factor and does not equal g as it would for free fall, but only g sin s.
Further Exploring
Multiplication of one vector by another opens up new areas of applications, but we won't discuss it here. Suffice to say that (at least) two different kinds of multiplication are in wide use--scalar multiplication where the result is an ordinary number or a "scalar" ("scalar quantity"), and vector multiplication where the result is a different vector, perpendicular to the other two.
Here is an example of an application of scalar multiplication
Questions from Users:
***
What's the difference between speed and velocity?
|
 So far this is just a complicated way of doing something obvious. What makes "arrow addition" useful is that it also holds when directions are different. Suppose the airplane flies into a headwind of 100 mph: we expect the velocity relative to the ground to be
So far this is just a complicated way of doing something obvious. What makes "arrow addition" useful is that it also holds when directions are different. Suppose the airplane flies into a headwind of 100 mph: we expect the velocity relative to the ground to be

