|
La question à résoudre est : Dans quelles conditions le satellite, situé en C,reste il stable par rapport à la Terre et la Lune ?
Le calcul est plus facile dans le cadre de la rotation de la Lune. Dans ce cadre, si un satellite en C est en
équilibre, il restera toujours à la même distance de la Lune ou de la Terre. Le centre de rotation des 3 points est le point D, la Terre elle même tourne autour de lui. Si le vaisseau spatial, en C, reste stabilisé, les trois corps ont la même période orbitale T. Si C est immobile dans ce cadre en rotation, il n'est pas soumis à la force de Coriolis (qui agit seulement sur des objets se déplaçant dans
ce cadre ), mais il sera soumis à la force centrifuge, aussi bien celle de la Lune que celle de la Terre.
Mettons en équations -- Equations qui visent à trouver les distances et les angles
(1) Noter d'abord que le rayon de rotation R du vaisseau spatial sera
différent de celui de la Lune, qui est, comme déja vu :
c/(1 + m/M)
Notons V la vitesse de rotation de la Lune, et v celle du vaisseau spatial. Puisque Distance = vitesse x
temps
2π R = vT
2π c/(1 + m/M) =
VTOn en tire
2π/T = v/R
2π/T = (V/ c)(1 +
m/M)
Ces deux expressions égales à 2π/
T sont aussi égales l'une à l'autre, d'où
(1)
v/R = (V/c)(1 +
m/M)
Cela exprime simplement le fait bien connu que si deux objets tournent conjointement, le plus éloigné de l'axe est plus rapide . Les vitesses sont proportionnelles aux distances à l'axe.
(2) La force centrifuge sur la Lune est
mV2/[c/(1 + m/M)] =
m(V2/c)(1 + m/M)
Et elle est équilibrée par l'attraction de la Terre
GmM/c2
où G est la constante de gravitation de Newton, mesurée pour la première fois par Henry Cavendish. Dans une orbite circulaire, les deux facteurs sont égaux et s'équilibrent (comme dans le calcul de la section 20):
GmM/c2 = m(V2/c)(1 +
m/M)
En divisant les deux termes par (m/c) on obtient une deuxième équation :
(2)
GM/c = V2 (1 +
m/M)
(3) Si m' est la masse du vaisseau spatial, la force centrifuge qui s'y applique est :
m' v2/R
Elle est équilibrée par la force
Fe d'attraction de la Terre et Fm celle de la Lune. Néanmoins, seules les composantes de ces forces situées sur la ligne
R s'opposent efficacement à cette force centrifuge. D'ou :
m'v2/R = Fm cosβ +
Fe cosα
Et selon la théorie de Newton de la gravitation :
Fm = G m'm/a2
Fe = G m'M/b2
Si dans la dernière équation, juste au dessus, on remplace par cette équivalence, et si on divise par
m' les deux côtés, on obtient une 3ème équation :
(3)
v2/R =
(Gm/a2) cosβ +
(GM/b2) cosα
(4) Finalement, les forces s'appliquant au vaisseau spatial
perpendiculairement à R doivent s'annuler. Si non, le vaisseau spatial suivrait la plus importante, ne resterait pas en C, et ne serait donc plus en équilibre. Il faut donc que :
Fm sinβ = Fe
sinα
Après substitution et division des deux côtés par Gm', il reste :
(4)
(m/a2) sin β
= (M/b2) sin
α
Récapitulons l'ensemble des équations :
- v/R =
(V/c)(1 + m/M)
- GM/c =
V2 (1 + m/M)
-
v2/R = (Gm/a2) cos β+ (GM/b2) cos α
-
(m/a2) sinβ =
(M/b2) sinα
3 types de quantités apparaissent ci.
- ---Certaines sont connues et constantes --G, m et M.
Leurs valeurs sont données et nous ne nous attendons pas à ce qu'elles changent.
- --Certains sont les distances--r, a, b et
c--elles dépendent des positions de la Terre, de la Lune et du vaisseau spatial dans l'espace. Les angles (
α,β) dépendent aussi de ces distances, mais nous n'aurons pas besoin de les connaître exactement.
- --Et certaines sont des vitesses, à savoir v et
V.
Il faut arriver à éliminer ces vitesses, pour se mettre dans dans des conditions purement géométriques, n'impliquant que des distances et des angles.
Nous avons précédemment déjà effectué une élimination à propos de deux équations comprenant la période orbitale T, qui équivalait chacune à 2π/T. En rapprochant ces deux expressions égales, nous avons obtenu une expression plus simple, ne contenant plus T (dans un processus d'élimination, on renonce toujours à une équation: on commence avec deux, on termine avec une seule.)
Il faut suivre ici la même démarche et éliminer V entre (1) et (2) pour obtenir une équation n'impliquant que v. Puis nous éliminerons v entre ce résultat et (3), pour obtenir une équation ne comportant plus de vitesses, comme (4), qui ne contient plus ni v ni
V.
| Dans (1), portez au carré les deux côtés :
v2/R2 =
(V2/c2) (1 + m/M) 2
Multipliez les deux côtés par c2 Et divisez-les par (1 +
m/M)
v2 (c2/R2)/[1 +
m/ M] = V2 (1 + m/M)
A rapprocher de (2)
GM/c = V2 (1 + m/M) On peut donc égaliser :
(5)
v2
(c2/R2) /[1 + m/M] = GM/c
et V vient d'être éliminé. Multipliez maintenant les deux côtés par (1
+ m/M), divisez-les par c2 et multipliez-les par
R
v2/R = (GM/ c3)R (1 +
m/M) A rapprocher de (3)
v2/R = (Gm/a2) cosβ + (GM/b2) cos
α
Donc ( multipliantR d'un facteur 1/c)
(GM/c2) (R/c) (1 + m/M) =
(Gm/a2) cosβ +
(GM/b2) cosα
En divisant le tout par GM on retrouve une des équations de départ, et une autre, qui est (4)
(6) (1/c2) (R/c) (1 +
m/M) = (1/a2)(m/M) cosβ+ (1/b2) cosα
(4) (m/a2)
sinβ = (M/b2) sinα
Plutôt compliqué! Cependant, si nous avons déjà jeté un coup d'œil sur la réponse nous pensons qu'il y auraient d'heureuses surprises si le triangle ABC était équilatéral, avec ses angles valant tous 60 ° et ses côtés égaux, tous d'une même longueur, que nous noterons r:
a = b = c = r
Dans ce cas, si les équations ci-dessus sont multipliées par
r2, les facteurs (1/a2),
(1/b2) et (1/c2) disparaissent ! Laissant :
(7) (R/c)(1 + m/M) =
(m/M)cosβ + cosα
(8) m sinβ
= M sinα
Ou
m/M = sinα /sinβ
Substituons dans le terme droit de (7)
(R/c)(1 + m/M) = (sinα
cosβ/sinβ) +
cosα Multiplions par sinβ
sin β
(R/c)(1 + m/M) = sinα cosβ + cosα sinβ
= sin(α +
β) = sin C = sin B
Cette dernière égalité s'obtient parce que les trois angles (A, B, C) sont égaux .
Divisons maintenant les deux termes par R, et redisposons
:
sin β/[cM/(M+m)] = sin
B/ R
C'est la loi des sinus dans le triangle CDB, et est donc évidemment certain. En reprenant en arrière, on peut maintenant prouver que toutes les équations précédentes, de (1) à (4), sont satisfaites si ABC est équilatéral. Par conséquent C est un point d'équilibre dans cette référence tournante. Si nous n'avions pas posé ABC comme équilatéral, et les distances (a,b,c) nous aurions obtenu une relation différente de la loi des sinus, sans vérification possible, et l'ensemble des équations exigées pour l'équilibre au point C n'auraient donc pu être satisfaites.
Comme il a déjà été signalé, L4 et L5 sont des points d'équilibre stable, et on les a proposé comme emplacements de grandes "colonies de l'espace", monobloc, à partir d'une idée développée et préconisée par le défunt Gerald o'Neill. En 1978 Higgins et Barry Gehm ont même écrit pour les colons potentiels une "complainte de L5" :
"Home on Lagrange" sur l'air de "Home on the range". Voici son commencement : cela donne à peu près ceci :
Repaires de Lagrange
Oh, donnez moi un lieu
où les gravitons se focalisent
où le problème trois corps soit résolu
où les micro-ondes jouent
sous 3 degrés K
Et les froids virus n' évolueront jamais.
CHOEUR:
repaires, repaires de Lagrange
Là où les débris de l'espace se rassemblent toujours...
|
NOTE. Le "problème des trois corps" est la recherche de la solution du mouvement de trois corps s'attirant mutuellement. Il est célèbre parce que les astronomes ont buté sur lui pendant de nombreuse d'années. Le roi de Suède avait même offert un prix à qui le résoudrai : le prix a été revendiqué par le mathématicien français Henri Poincaré, qui a prouvé qu'en général il est insoluble - qu'aucune formule explicite ne peut prévoir le mouvement dans un avenir indéfini. Dans la terminologie d'aujourd'hui,on dirait que le mouvement général des trois corps a des propriétés chaotiques. Même dans un problème à la limite de celui " des trois corps", où l'un est très petit - par exemple, terre, Lune et vaisseau spatial - il n'y a pas de solution. (Sauf cas particuliers, comme ceux dans lesquels le vaisseau spatial est placé à un des points de Lagrange ).
En savoir plus :Sur les rassemblements spatiaux aux points de Lagrange :
- Gerald K. O'Neill, "The Colonization of Space", Physics Today
September 1974, p. 32.
- Gerard K. O'Neill, "The High Frontier", William Morrow and Co., NY,
1977; Anchor Books (Doubleday) 1982.
Sur L4 et L5 et les astéroïdes bloqués au voisinage de L4 et L5 du système de Jupiter - soleil : "When Trojans and Greeks Collide"
by I. Vorobyov, Quantum, September-October 1999, p. 16-19. Cet article contient une autre démonstration de l'équilibre des mouvement en L4 et L5, plus générale (aucune limitation sur les masses), mais utilise un système de référence en rotation et des vecteurs bidimensionnels. Ce calcul peut être trouvé dans la section (34-c) de ce site Web.
En option: #34c Un autre calcul pour les points L4 et L5
(voir le paragraphe ci dessus).
Prochaine étape:#35 Vers les Planètes, vers les Etoiles
Chronologie
Glossaire
Revenir
à la liste principale
Auteur et responsable : Dr. David P.
Stern
Mail au Dr.Stern: stargaze("at" symbol)phy6.org
Traduction française: Guy Batteur guybatteur(arobase)wanadoo.fr
Dernière mise à jour : 5.25.2004
|
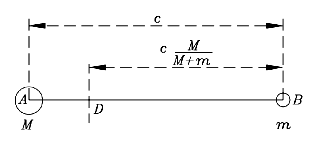 Comme indiqué dans la
Comme indiqué dans la 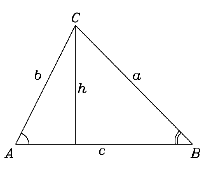 On peut le démontrer pour les angles A et B, en menant à partir du troisième angle C une perpendiculaire au côté opposé du triangle.
Si
h est la longueur de cette ligne. Il vient
On peut le démontrer pour les angles A et B, en menant à partir du troisième angle C une perpendiculaire au côté opposé du triangle.
Si
h est la longueur de cette ligne. Il vient
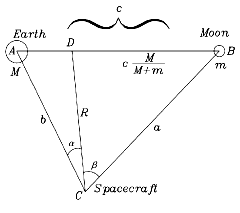 Au schéma déjà présenté pour montrer le centre de masse du système terre- lune, nous ajoutons un vaisseau spatial au point C, à une distance b de la Terre, a de la Lune et R
du centre de masse D. Comme dans la loi des sinus, nous nommons les angles (A, B, C) et les côtés
(a,b,c) . Les dénominations analogues se font face.
Au schéma déjà présenté pour montrer le centre de masse du système terre- lune, nous ajoutons un vaisseau spatial au point C, à une distance b de la Terre, a de la Lune et R
du centre de masse D. Comme dans la loi des sinus, nous nommons les angles (A, B, C) et les côtés
(a,b,c) . Les dénominations analogues se font face.