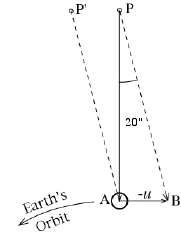
Seen from the boat, the flag always points to the rear, because in the boat's frame of reference, a wind with velocity –u seems to be blowing. It always points in the same direction.

What if the day is not windless? If a wind is blowing with velocity v? In the frame of the boat, the air now moves with velocity v – u , a vector sum, with the direction of v specified relative to the boat ("in the boat's frame"). The flag now points neither downwind, nor to the rear, but somewhere in between.

Suppose the boat now changes direction. In the frame of the boat u is still directed to the rear, but the wind now seems to come from a different direction, relative to the boat. Consequently, the direction of v changes, and the flag, pointing alongthe new v – u, has a different direction as well. For more about this effect, see here

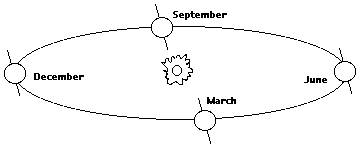
Apparent Displacement of Stars

This section is about starlight, not about boats and flags. From Newton's days, astronomers have tried to find how far the stars were by the parallax method, using the diameter of the Earth's orbit as a baseline. They carefully measured the positions of stars at times half a year apart--representing two positions of the Earth separated by 300,000,000 km--and then checked whether the positions of stars in the sky changed. They soon found that, indeed, the positions did change. The trouble was that the observations did not make much sense.

Jean Picard, one of the early French astronomers, made possible precise observations by introducing crosshairs in the telescope eyepiece. With this instrument he noted around 1680 that the observed positions of stars were not always the same. John Flamsteed, the astronomer royal of Britain--head of the Royal Observatory in Greenwich--confirmed those shifts. For instance Polaris, the pole star, seemed to travel annually around an ellipse whose width was 40", 40 seconds of arc.

As discussed in the section on parallax, that might suggest that the distance to Polaris was 1/40 of a parsec or less than 0.1 light year. However, the shifts in position did not occur at the times they were expected . The greatest shift of Polaris in any given direction occured not when the Earth's was at the opposite end of its orbit, as it should have been, but 3 months later.

For instance, in the drawing above, the apparent position of Polaris should have been shifted the furthest in the direction of "December" when Earth was in its "June" position, which is as far as it can go in the opposite direction. Instead, it happened in September, when the Earth had moved 90° from its position in June. In hindsight, the important quantity was not the displacement of Earth, but its velocity, which in September pointed towards the direction towards which Polaris was displaced.

Bradley's Explanation

Astronomers were greatly puzzled, the more so when it turned out that all other stars near Polaris were shifted the same way. Then in 1729 the British astronomer royal, James Bradley, took a boat trip on the river Thames near London and noted the strange behavior of the flag on top of the boat's mast: it pointed neither downwind nor to the back of the boat, but in some direction in between, and when the boat changed course, that direction changed, too.

A sudden inspiration came to Bradley. The flag sensed a combination of two air flows, as seen in the frame of the boat: one due to the wind, the other due to the boat's motion. In a similar way, he reasoned, the velocity of the light coming from Polaris was modified in our own frame, by the added velocity of the Earth!

The velocity of light--today universally denoted by the letter c, as in "E=mc²"-- had been estimated in 1675 by Ole Romer, a Dane working at the Paris observatory, from a study of the eclipses of a moon of Jupiter. The velocity u of Earth in its orbit was also approximately known. Viewed from the frame of the moving Earth, the rest of the universe had a velocity –u, perpendicular to the velocity c of light coming from Polaris. Add these two up, as vectors, and you get the observed displacement.

–u

direction

Let us calculate

In the drawing shown here, let A be the Earth and AP the direction towards Polaris (the star itself is much more distant). The vector PA represents the velocity of light coming from Polaris at c=300,000 km/s. The vector AB represents the velocity –u of Polaris relative to Earth, equal in size to the Earth's velocity u=30 km/s in its orbit, but in opposite direction. (To simplify the calculation we assume AP is perpendicular to AB, in which case the apparent motion of the star is a circle; actually the angle is usually less than 90° making the apparent motion not a circle but an ellipse.) The point P ' indicates the apparent direction of Polaris as viewed from Earth, offset by an angle a=40" from its actual direction.

The length of each side in the triangle ABP is proportional to the velocity it represents; obviously its dimensions are not drawn to scale (it would be hard to draw a triangle with one side 10000 times longer than the other!). If the triangle is viewed as a pie-slice from a circle and the angle at P is denoted by α, we get

30/(2π 30,000) = 30 / 60,000 π = α/360°

α = 10800 / 60000π = 5.7296 / 1000 degrees.

Each degree contains 60 minutes of arc (60') and each minute has 60 seconds of arc (60"), units unrelated to the minutes and seconds of time. Each degree thus equals 3600", giving

α = 3600" (5.7296 / 1000) = 20.6"

Half a year later the direction of u is reversed and the displacement is in the opposite direction, giving an annual range of about 40", as observed.

Aberration of the Solar Wind

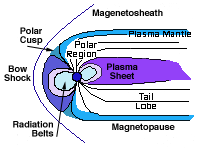Strictly speaking, the solar wind is a plasma, a mixture of free electrons and of positive ions, atoms which have lost electrons in the violent collisions experienced in a 1,000,000 degree gas. Being a plasma, it can conduct electric currents and its particles can be steered by magnetic fields. The Earth's magnetism, in particular, deflects the solar wind flow, creating an elongated cavity known as the magnetosphere, from which the solar wind is excluded (see picture). On the side facing the Sun, the solar wind only reaches within 10-11 Earth radii of the Earth's center (65-70,000 km) before it is deflected sideways. On the night side, facing away from the Sun, a long "magnetic tail" extends to great distances, along the flow direction of the solar wind.

But what is that direction? In the reference frame of the Sun, the solar wind on the average streams radially outwards, with a velocity v of about 400 km/s (it does not change with distance). The Earth, however, orbits the Sun with a velocity u perpendicular to v, of about 30 km/s. Viewed from the frame of the Earth, a velocity -u is then added to v, so to us the solar wind appears to move with v' = v-u, as the drawing shows. The magnitude v' of the new velocity is found by applying the theorem of Pythagoras to the triangle ABC, which gives

(v')² = v² + u² v' = 401.12 km/s

If <β is the angle by which the solar wind is shifted in the Earth's frame, then

sin β = 30/401.12 = 0.0749 (or else, tan β = 30/400 = 0.075)

β = 4.289°

With a spacecraft exploring the distant nightside tail, as the Japanese "Geotail" did (at distances around 200 Earth radii), this effect must be taken into account if we wish to place the spacecraft in the tail and not next to it. Unfortunately, the direction of v also varies randomly by a few degrees, so that, while taking b into account helps, sometimes a point calculated to be inside the tail still misses it.

A much greater aberration effect is expected aboard the solar probe spacecraft, planned by NASA for observing the solar wind near the Sun. Its orbit will make it approach the Sun within 4 solar radii, where it avoids melt-down in the intense heat only by hiding behind a specially designed heat shield.

How then, one may well ask, can one shield out the sunlight and yet observe the solar wind, which like sunlight flows radially outwards? That is where aberration helps. At closest approach (perihelion) the solar probe would move at about 300 km/s, so that the solar wind moving at 400 km/s (but not sunlight) would be aberrated by about 37°, allowing it to reach detectors protected behind the heat shield.

Postscript: Space Data by Laser

Miniature satellites have trouble transmitting data to the ground. The satellite may be small, but the radio power it needs depends on the distance and cannot be arbitrarily reduced.

One proposed solution (as told to me by Dr. Arthur Peschek) was to use a laser on the ground. Instead of a radio transmitter, the satellite carries a corner reflector prism, which bounces the beam right back in the direction it came. This had been tried with a laser reflector left by astronauts on the Moon, and a big telescope on Earth did detect the returning beam. In the satellite, an electronic device using very little power would modulate the laser beam, encoding in it all the instrument data. Since the return beam retraces the path of the primary laser beam, the detecting station could be placed right next to the laser.

Pretty neat--huh? Yes--but only until the proposers realized that aberration (like Bradley's) would shift the returning beam, because the satellite (unlike the Moon) moves quite rapidly. The shift may amount to tens or hundreds of meters, and its direction depends on the satellite's motion. Because of it, the idea was dropped.

Optional: #22b The Theory of Relativity

Next stop: #22c Airplane Flight

Timeline Glossary Back to the Master List

Author and Curator: Dr. David P. Stern
Greenbelt, Maryland Mail to Dr.Stern: stargaze("at" symbol)phy6.org .

Updated: 9-22-2004 ; reformatted 24 March 2006 ; later update 13 October 2016