#21c     Flight to Mars: Calculations

    In the preceding section the route to Mars was identified, along a Hohmann Transfer Ellipse. The time required was derived, about 8.5 months, as well as the position of Mars at the time of launch, about 45° past closest approach.

    This section calculates two essential details: the velocity boost needed to inject the Mars spaceship into the transfer orbit, and the arrival velocity at the orbit of Mars. Will the spaceship be overtaking the planet or be overtaken by it, and what will be the velocity mismatch between ship and planet--a mismatch which will probably require an additional rocket firing? Keep reading, and if you can handle elementary algebra, you may find out.

Notation and Escape Velocities

    Before starting out, it helps to establish a notation for the quantities involved here. Even though some of them are vectors, only their magnitudes are handled. Bold face is only used to accentuate, never to indicate vector character.

    As before, r₁ = 1 AU is the distance of Earth from the Sun, r₂ = 1.523691 AU that of Mars, and (as an approximation) both planets are assumed to move in circles.

    Velocity V will be measured in kilometers per second (km/s), and different velocities are identified by subscripts. Lower-case v identifies velocities associated with orbits around Earth rather than around the Sun.

    The preceding section already introduced the orbital velocity V₀ of Earth around the Sun, amounting to about 30 km/s, much larger than v₀ ~ 8 km/s (approx.) required by a satellite circling the Earth just above the surface(ignoring the atmosphere!). In section #21 it was noted that the escape velocity v_e from such a low orbit is obtained by multiplying v₀ by the square root of 2, equal to 1.41421356.... approximated here by 1.414. This gives
   

    Such a spacecraft, however, is still not free to move to any point in space. The velocity v_e has purchased its freedom from the Earth's gravity, but not freedom from the pull of the Sun, around which it continues to move in an orbit similar to Earth's, at approximately V₀ =30 km/s.

    The situation is now completely analogous to escape from a low altitude Earth orbit (only the cost is higher!). To break free from a circular orbit around the Sun and leave the Solar system, the spacecraft needs to boost its velocity to a "second escape velocity"
   

    To reach V_e it must somehow increase its velocity by an additional 12.42 km/s--more than is needed to escape the Earth's gravity, starting from rest on the surface! Luckily, ways exist (discussed in Section #35) of making the motion of planets (or of the Moon) provide part of this boost.

    Other velocities entering the calculation are the velocity V₁ with which the spaceship starts from near Earth and enters the Hohmann ellipse (distance r₁ from the Sun), and the velocity V₂ with which it reaches the orbit of Mars (distance r₂). Also, V₃ will be the velocity of Mars in its orbit, assuming it has a constant magnitude (i.e assuming the orbit of Mars is circular).

   If V₂ > V₃, the spaceship overtakes Mars, while with V₂ < V₃ it is being overtaken.

Required Equations

    (1) Kepler's Laws

•     The first law is "Planets move in ellipses, with the Sun at one focus. " That is already being used, e.g. the transfer ellipse is one such orbit.

•     The second law is "The line connecting a planet to the Sun sweeps equal areas in equal times. " Let us try to extract from this a useful equation.

Application of Kepler's 2nd law

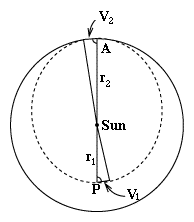
    The drawing here shows the orbit of Mars (solid) and the transfer ellipse (broken line), with radiuses (r₁, r₂) to the (perigee, apogee) points, at which the spacecraft velocity is (V₁, V₂). The short segments drawn at these locations represent the distance covered by the spacecraft in the next second after passing perigee or apogee, and by the definition of velocity ("distance per second") they also equal V₁ and V₂. Actually, those segments should be curved like the orbit, but being so short they differ negligibly from straight lines We then complete the long thin triangles, which have these lines as bases.

    Note that each of these triangles has a right angle at its bottom, because at apogee and at perigee (and nowhere else), the line to the Sun is perpendicular to the orbit.

    At perigee, the height of the triangle is r₁, the length of its base is V₁, so by the equation for the area A₁ of a triangle
   

    Each of these triangles is swept in one second, so by Kepler's 2nd law their areas can be set as equal. Multiplying both sides of that equality by 2 yields

    The equation is numbered to help refer to it later. Please note this relation only holds between apogee and perigee. At other points of the orbit, the angle between the radius and the orbit is not 90⁰, and the area also depends on its exact value.

    Kepler's third law was already used in determining the orbital period. It will be needed again at the end.

    (2) The Energy Equation

    In section #12 it was stated that the energy E of a satellite of mass m orbiting Earth, at any point in its orbit, is

    As noted earlier, for an object in the Earth's orbit to completely escape the Sun (but just barely!), it needs a velocity V_e = 1.414..V₀ = 42.42 km/s. Let E₀ be the energy of such an object. Then since

    Because it has escape velocity, if we wait a long, long time, this object will be extremely far from Earth, and, having exhausted practically all of its kinetic energy, its velocity will be very close to zero. Then both terms on the right side of equation (2) tend to zero, suggesting
   

    Dividing by m and shifting the negative V_e term to the right
   

    from which the value of k may be written
   

Calculation

    Returning now to the spaceship in a Mars transfer orbit, its energy should be the same at the perigee P and the apogee A, so by equation (2)

    Divide both sides by m ("cancel m") and multiply both sides by 2

    Substituting this on the left side of (4)

        V₁² – V₂²   =   V₁² (1   –   (r₁²/r₂²)) =                            

                  =   V₁² (1 – (0.656301)²   =   0.569269 V₁²   =   609.834 (km/s)²

Dividing both side by 0.569269

Arrival at Mars

    It has given up some of its kinetic energy to overcome the pull of the Sun and moV_e further outward from the Sun. The big question now is--how does this compare with the velocity V₃ of Mars in its orbit?

    To derive a velocity in km/s, distances must be ultimately rendered in kilometers and times in seconds, but "for the benefit of pedestrians," we break up the calculation, avoiding big numbers and scientific notation. We start with Kepler's 3rd law for circular orbits, with distance r in AU and orbital period T in years. As derived in the preceding section (and also in section #10), in these units

    For Mars, r = 1.523691, T² = (1.523691)³ = 3.53745

Assuming 365.25 days per (Julian) year:

    During that time the spaceship covers

    Dividing by T, this comes to

Each day has (24)(3600) = 86400 seconds, so the orbital distance covered by Mars each second is

    Distance-per-second is of course the definition of velocity. Therefore
   

we see that Mars is the one moving faster, and will be overtaking the spaceship. To match velocities with Mars, the spaceship must generate an extra boost of 2.649 km/s .