|
We choose the points A and B to be not on the edge ("limb") of the Sun's disk during 2nd and 3rd contact, but at the center of Venus at those times. If O is the center of the Sun, these points lie on a circle around O with radius (R–r). Thus the time for covering AB marks the passage of Venus across a chord (=straight cut across a circle) of a "reduced Sun" covering only 30.5 minutes of arc.
We will also need a moderately accurate value of the distance h of the line AB from the center O, or more conveniently the angle θ (Greek theta; see Fig. 4 below), half the angle covered by AB. Deriving it from published photographs (e.g. the published version of Fig. 1 of the preceding page, or plots like the one provided by the U. of Lancashire) gives about 46.4 degrees. Then (Figure 4 below)
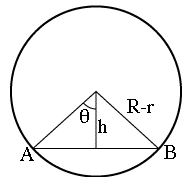 |
| Fig. 4 Variables used in the calculation
|
h = (R–r) cos θ
(1)
Since the transit time T is proportional to the distance (AB), we can write
T = k·AB
where k is some proportionality factor. Its value will not be needed, since we aim to use the ratio between T and the difference ΔT in transit times observed at two locations, and in deriving the ratio, k cancels out. Using trigonometry
T = 2k (R–r) sinθ
(2)
If the line A'B' of the other station is slightly longer, it covers a slightly larger angle 2(θ+δ), and its distance from O is not h but
h' = (R–r) cos (θ+δ)
= (R–r)(cosθ cosδ – sinθ sinδ ) (3)
If δ is a very small angle, sinδ is also small. But even when a small value of sinδ remains important enough to be included, cosδ is probably so close to 1 that one can safely replace it by 1. To demonstrate this, note that
cos2δ= 1 – sin2δ
Recalling that the square root is also the (1/2) power, by the binomial theorem
cosδ= (1 – sin2δ)1/2
~ 1 – (1/2)sin2δ
So if we approximate cosδ by 1, the error made is only of the order of sin2δ which (as is true for numbers much smaller than 1) is much smaller than sinδ . If in expressing h', we keep sinδ but replace cosδ with 1, then to a good approximation
h' = (R–r)(cosθ – sinθ sinδ )
from which
D = h –h' = (R–r) sinθ sinδ
(4)
The transit time at point P' is obtained in a similar way to equation (2)
T ' = 2k (R–r) sin (θ+δ) =
= 2k (R–r)(sinθ cosδ + cosθ sinδ )
and to the same good approximation as before, with the angle δ small
T ' = 2k (R–r)(sinθ + cosθ sinδ)
= T + 2k (R–r) cosθ sinδ
making the difference
ΔT = T ' – T = 2k (R–r) cosθ sin δ
(5)
Thus
ΔT/T = 2k (R-r) cosθ sinδ / 2k (R–r) sin θ
= cosθ sinδ / sin θ
(6)
This is just about what was expected: the smallness of the ratio on the left is balanced by the smallness of sinδ on the right. Extracting that term
sinδ = [sinθ / cosθ] ΔT / T
(7)
This can be substituted in equation (4) for D, another small term
D = (R–r) [sin 2θ / cosθ] ΔT / T
(8)
That is what was needed. As Halley suggested, the separation D between transit tracks is now expressed in terms of the observed difference between transit times, as well as the length of the observed transit time T (or its average (T + T')/2) as well as the angle θ, giving the distance of the transit path from the center of the Sun
|